前言

什么是数据结构？

数据结构的定义

  • 官方定义

    无

  • 民间定义

    • “数据结构是数据对象，以及存在于该对象的实例和组成实例的数据元素之间的各种联系。这些联系可以通过定义相关的函数来给出。” — 《数据结构、算法与应用》
    • “数据结构是ADT（抽象数据类型 Abstract Data Type）的物理实现。” — 《数据结构与算法分析》
    • “数据结构（data structure）是计算机中存储、组织数据的方式。通常情况下，精心选择的数据结构可以带来最优效率的算法。” —中文维基百科

  • 从自己角度认识

    在计算机中，存储和组织数据的方式。

数据结构在生活中应用

我们知道，计算机中数据量非常庞大，如何以高效的方式组织和存储呢?

例如：一个庞大的图书馆中存放了大量的书籍，我们不仅仅要把书放进入，还应该在合适的时候能够取出来。

图书摆放要使得两个相关操作方便实现：

  • 操作 1：新书怎么插入？
  • 操作 2：怎么找到某本指定的书？

图书各种摆放方式：

  • 方法 1：随便放

    • 操作 1：哪里有空位放哪里。
    • 操作 2：找某本书，累死。

  • 方法 2：按照书名的拼音字母顺序排放

    • 操作 1：新进一本《阿 Q 正传》， 按照字母顺序找到位置，插入。
    • 操作 2：二分查找法。

  • 方法 3：把书架划分成几块区域，按照类别存放，类别中按照字母顺序

    • 操作 1：先定类别，二分查找确定位置，移出空位。
    • 操作 2：先定类别，再二分查找。

结论：

  • 解决问题方法的效率，根据数据的组织方式有关。
  • 计算机中存储的数据量相对于图书馆的书籍来说数据量更大，数据更加多。
  • 以什么样的方式，来存储和组织我们的数据才能在使用数据时更加方便呢?
  • 这就是数据结构需要考虑的问题。

常见的数据结构

  • 数组（Aarray）
  • 栈（Stack）
  • 链表（Linked List）
  • 图（Graph）
  • 散列表（Hash）
  • 队列（Queue）
  • 树（Tree）
  • 堆（Heap）

注意：数据结构与算法与语言无关，常见的编程语言都有直接或间接的使用上述常见的数据结构。

什么是算法？

算法（Algorithm）的定义

  • 一个有限指令集，每条指令的描述不依赖于语言。
  • 接收一些输入（有些情况下不需要输入）。
  • 产生输出。
  • 一定在有限步骤之后终止。

算法通俗理解

  • Algorithm 这个单词本意就是解决问题的办法/步骤逻辑。
  • 数据结构的实现，离不开算法。

算法案例

假如上海和杭州之间有一条高架线，高架线长度是 1,000,000 米，有一天高架线中有其中一米出现了故障，请你想出一种算法，可以快速定位到处问题的地方。

  • 线性查找

    • 从上海的起点开始一米一米的排查，最终一定能找到出问题的线段。
    • 但是如果线段在另一头，我们需要排查 1,000,000 次，这是最坏的情况，平均需要 500,000 次。

  • 二分查找

    • 从中间位置开始排查，看一下问题出在上海到中间位置，还是中间到杭州的位置。
    • 查找对应的问题后，再从中间位置分开，重新锁定一半的路程。
    • 最坏的情况，需要多少次可以排查完呢? 最坏的情况是 20 次就可以找到出问题的地方。
    • 怎么计算出来的呢? log(1000000, 2)，以 2 位底，1000000 的对数 ≈ 20。

结论：

你会发现，解决问题的办法有很多，但是好的算法对比于差的算法，效率天壤之别。

大O表示法

什么是大O表示法

大O表示法可以告诉我们算法的快慢。

大O比较的是操作数，它指出了算法运行时间的增速。

O(n) 括号里的是操作数。

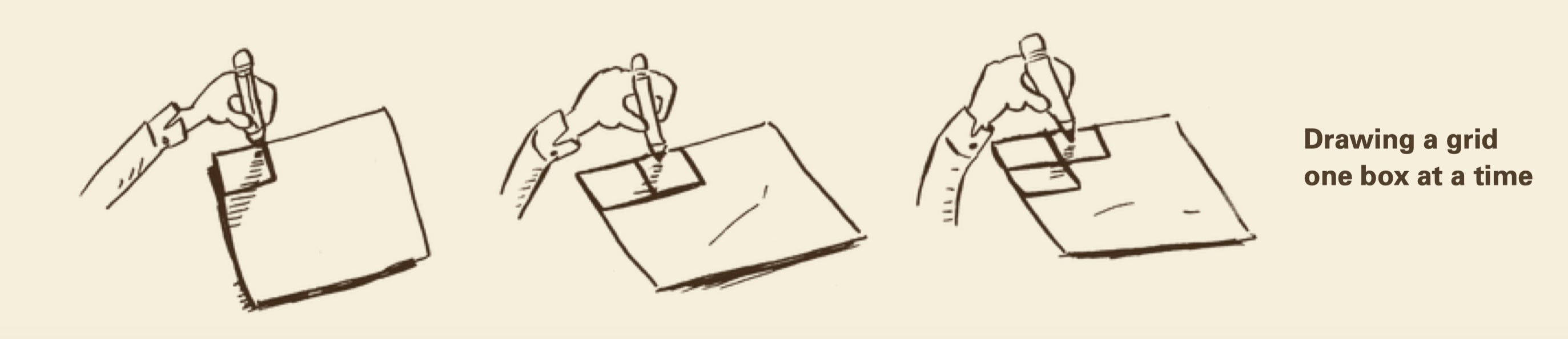
举例

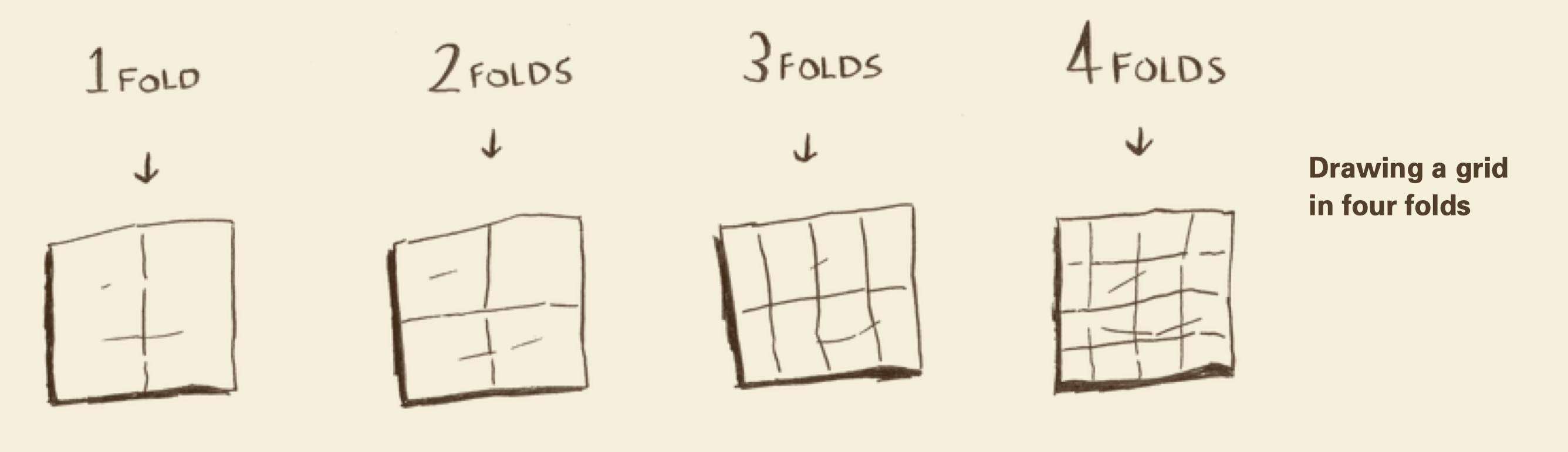
画一个16个格子的网格，下面分别列举几种不同的画法，并用大O表示法表示

  1. 一次画一个格子。O(n)

hiJNrT.png

  1. 折叠纸张，折叠四次就能出现16个格子。O(log n)

大O表示法所表示的是一个算法在最糟糕情况下的运行时间。

一些常见的大O运行时间

  • O(log n)，也叫对数时间，二分查找。
  • O(n)，也叫线性时间，简单查找。
  • O(n * log n)，快速排序——一种速度较快的排序算法。
  • O(n²)，选择排序——一种速度较慢的排序算法。
  • O(n!)，旅行商问题的解决方案——一种非常慢的算法。

hiJ8Gn.png

主要启示

  • 算法的速度指的是操作数的增速，而非时间。
  • 谈论算法速度说的是随着输入的增加，其运行时间将以什么样的速度增加。
  • 用大O表示法表示算法的运行时间。
  • 随着元素的增加，快算法比慢算法增加的速度是指数级的。比如，O(log n)和O(n)

补充

时间复杂度（一般情况？最坏情况？）

算法导论给出的解释：大O用来表示上界的，当用它作为算法的最坏情况运行时间的上界，就是对任意数据输入的运行时间的上界。

同样算法导论给出了例子：拿插入排序来说，插入排序的时间复杂度我们都说是O(n^2) 。

输入数据的形式对程序运算时间是有很大影响的，在数据本来有序的情况下时间复杂度是O(n)，但如果数据是逆序的话，插入排序的时间复杂度就是O(n^2)， 也就对于所有输入情况来说，最坏是O(n^2) 的时间复杂度，所以称插入排序的时间复杂度为O(n^2)。

同样的同理再看一下快速排序，都知道快速排序是O(nlogn)，但是当数据已经有序情况下，快速排序的时间复杂度是O(n^2) 的，**所以严格从大O的定义来讲，快速排序的时间复杂度应该是O(n^2)**。

但是我们依然说快速排序是O(nlogn)的时间复杂度，这个就是业内的一个默认规定，这里说的O代表的就是一般情况，而不是严格的上界。

我们主要关心的还是一般情况下的数据形式。

面试中说道算法的时间复杂度是多少指的都是一般情况。

不同数据规模的差异

我们说的时间复杂度都是省略常数项系数的，是因为一般情况下都是默认数据规模足够的大，基于这样的事实，给出的算法时间复杂的的一个排行如下所示：

O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n^2)平方阶 < O(n^3)(立方阶) < O(2^n) (指数阶)

但是也要注意大常数，如果这个常数非常大，例如10^7 ，10^9 ，那么常数就是不得不考虑的因素了。

O(logn)中的log是以什么为底？

平时说这个算法的时间复杂度是logn的，那么一定是log 以2为底n的对数么？

其实不然，也可以是以10为底n的对数，也可以是以20为底n的对数，但我们统一说 logn，也就是忽略底数的描述。

假如有两个算法的时间复杂度，分别是log以2为底n的对数和log以10为底n的对数，那么这里如果还记得高中数学的话，应该不难理解以2为底n的对数 = 以2为底10的对数 * 以10为底n的对数。

而以2为底10的对数是一个常数，在上文已经讲述了我们计算时间复杂度是忽略常数项系数的。

数组

几乎所有的编程语言都原生支持数组类型，因为数组是最简单的内存数据结构。

数组通常情况下用于存储一系列同一种数据类型的值。

但在 JavaScript 里，数组中可以保存不同类型的值。但我们还是要遵守最佳实践，别这么做（大多数语言都没这个能力）。

创建和初始化数组

  • new Array()

    1
    2
    3
    4
    5
    6
    7
    8
    9
    const daysOfWeek = new Array(
      "Sunday",
      "Monday",
      "Tuesday",
      "Wednesday",
      "Thursday",
      "Friday",
      "Saturday"
    );

  • []

    1
    2
    3
    4
    5
    6
    7
    8
    9
    const daysOfWeek = [
      "Sunday",
      "Monday",
      "Tuesday",
      "Wednesday",
      "Thursday",
      "Friday",
      "Saturday",
    ];

数组常见操作

添加元素

  • 添加一个元素到数组的最后位置 array.push(item)

  • 在数组首位插入一个元素 array.unshift(item)

  • 在指定索引位置插入元素 array.splice(index, 0, item)

    splice() 第二个参数为 0 时，表示插入数据。

    1
    2
    3
    4
    let myArray = [1, 2, 3];
    // 在 索引 0 的位置，插入 A
    myArray.splice(0, 0, "A");
    console.log(myArray); //--> ['A', 1, 2, 3]

删除元素

  • 删除数组最后的元素 array.pop(item)

  • 删除数组首位的元素 array.shift(item)

  • 删除指定索引位置的元素 array.splice(start, number)
    例如：

    1
    2
    3
    4
    let myArray2 = [1, 2, 3, 4, 5];
    // 删除索引 4 位置起，2 个元素
    myArray2.splice(4, 2);
    console.log(myArray2); //--> [1, 2, 3]

修改元素

  • 修改指定索引位置的元素 array.splice(index, 1, item)

    1
    2
    3
    4
    let myArray3 = [1, 2, 3, 4, 5, 6];
    // 修改 索引 1 的位置的元素为 AA
    myArray2.splice(1, 1, "AA");
    console.log(myArray3); //--> [1, "AA", 3, 4, 5, 6]

  • 修改指定索引位置的几个元素 array.splice(index, number, item)

    1
    2
    3
    4
    let myArray4 = [1, 2, 3, 4, 5, 6, 7];
    // 在 索引 2 的位置起，修改两个元素为 AA BB
    myArray2.splice(2, 2, "AA", "BB");
    console.log(myArray3); //--> [1, 2, "AA", "BB", 5, 6, 7]

栈

数组是一个线性结构，并且可以在数组的任意位置插入和删除元素。

但是有时候，我们为了实现某些功能，必须对这种任意性加以限制。

栈和队列就是比较常见的受限的线性结构。

什么是栈

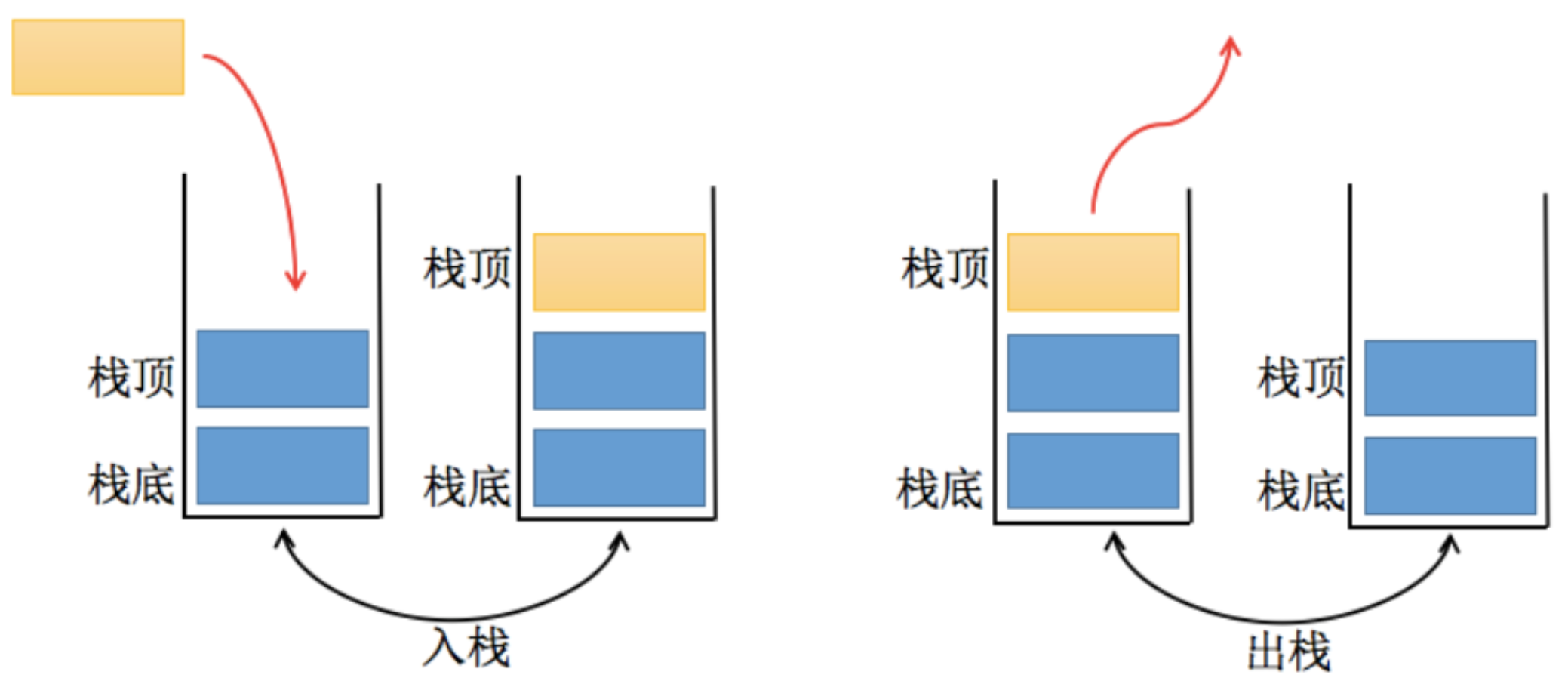
栈（stack）是一种运算受限的线性表：

  • LIFO（last in first out）表示就是后进入的元素，第一个弹出栈空间。类似于自动餐托盘，最后放上的托盘，往往先把拿出去使用。
  • 其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。
  • 向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；
  • 从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

如下图所示：
hiYXX6.png

栈的特点：先进后出，后进先出。

程序中的栈结构

  • 函数调用栈：A(B(C(D())))：
    即 A 函数中调用 B，B 调用 C，C 调用 D；在 A 执行的过程中会将 A 压入栈，随后 B 执行时 B 也被压入栈，函数 C 和 D 执行时也会被压入栈。所以当前栈的顺序为：A->B->C->D（栈顶）；函数 D 执行完之后，会弹出栈被释放，弹出栈的顺序为 D->C->B->A;

  • 递归：
    ==为什么没有停止条件的递归会造成栈溢出？比如函数 A 为递归函数，不断地调用自己（因为函数还没有执行完，不会把函数弹出栈），不停地把相同的函数 A 压入栈，最后造成栈溢出（Queue Overfloat）==。

练习

题目：有 6 个元素 6，5，4，3，2，1 按顺序进栈，问下列哪一个不是合法的出栈顺序？

  • A：5 4 3 6 1 2 （√）
  • B：4 5 3 2 1 6 （√）
  • C：3 4 6 5 2 1 （×）
  • D：2 3 4 1 5 6 （√）

题目所说的按顺序进栈指的不是一次性全部进栈，而是有进有出，进栈顺序为 6 -> 5 -> 4 -> 3 -> 2 -> 1。

解析：

  • A 答案：65 进栈，5 出栈，4 进栈出栈，3 进栈出栈，6 出栈，21 进栈，1 出栈，2 出栈（整体入栈顺序符合 654321）。
  • B 答案：654 进栈，4 出栈，5 出栈，3 进栈出栈，2 进栈出栈，1 进栈出栈，6 出栈（整体的入栈顺序符合 654321）。
  • C 答案：6543 进栈，3 出栈，4 出栈，之后应该 5 出栈而不是 6，所以错误。
  • D 答案：65432 进栈，2 出栈，3 出栈，4 出栈，1 进栈出栈，5 出栈，6 出栈。符合入栈顺序。

栈结构实现

栈常见的操作

  • push() 添加一个新元素到栈顶位置。
  • pop() 移除栈顶的元素，同时返回被移除的元素。
  • peek() 返回栈顶的元素，不对栈做任何修改（该方法不会移除栈顶的元素，仅仅返回它）。
  • isEmpty() 如果栈里没有任何元素就返回 true，否则返回 false。
  • size() 返回栈里的元素个数。这个方法和数组的 length 属性类似。
  • toString() 将栈结构的内容以字符串的形式返回。

JavaScript 代码实现栈结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// 栈结构的封装
class Stack {
  constructor() {
    this.items = [];
  }

  // push(item) 压栈操作，往栈里面添加元素
  push(item) {
    this.items.push(item);
  }

  // pop() 出栈操作，从栈中取出元素，并返回取出的那个元素
  pop() {
    return this.items.pop();
  }

  // peek() 查看栈顶元素
  peek() {
    return this.items[this.items.length - 1];
  }

  // isEmpty() 判断栈是否为空
  isEmpty() {
    return this.items.length === 0;
  }

  // size() 获取栈中元素个数
  size() {
    return this.items.length;
  }

  // toString() 返回以字符串形式的栈内元素数据
  toString() {
    let result = "";
    for (let item of this.items) {
      result += item + " ";
    }
    return result;
  }
}

测试封装的栈结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// push() 测试
stack.push(1);
stack.push(2);
stack.push(3);
console.log(stack.items); //--> [1, 2, 3]

// pop() 测试
console.log(stack.pop()); //--> 3

// peek() 测试
console.log(stack.peek()); //--> 2

// isEmpty() 测试
console.log(stack.isEmpty()); //--> false

// size() 测试
console.log(stack.size()); //--> 2

// toString() 测试
console.log(stack.toString()); //--> 1 2

栈结构的简单应用

利用栈结构的特点封装实现十进制转换为二进制的方法。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function dec2bin(dec) {
  // new 一个 Map，保存余数
  const stack = new Map();

  // 当不确定循环次数时，使用 while 循环
  while (dec > 0) {
    // 除二取余法
    stack.push(dec % 2); // 获取余数，放入栈中
    dec = Math.floor(dec / 2); // 除数除以二，向下取整
  }

  let binaryString = "";
  // 不断地从栈中取出元素（0 或 1），并拼接到一起。
  while (!stack.isEmpty()) {
    binaryString += stack.pop();
  }

  return binaryString;
}

测试

1
2
3
// dec2bin() 测试
console.log(dec2bin(100)); //--> 1100100
console.log(dec2bin(88)); //--> 1011000

队列

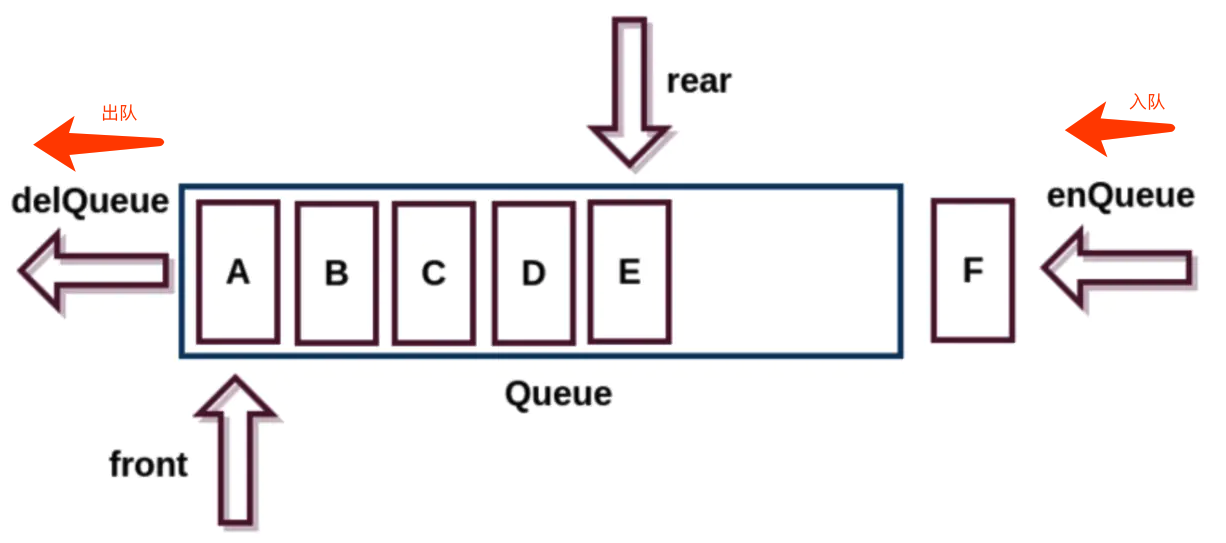
认识队列

队列（Queue）是一种运算受限的线性表，特点：先进先出。(FIFO：First In First Out)

受限之处：

  • 只允许在表的前端（front）进行删除操作。
  • 只允许在表的后端（rear）进行插入操作。

生活中类似队列结构的场景：

  • 排队，比如在电影院，商场，甚至是厕所排队。
  • 优先排队的人，优先处理。 (买票、结账、WC)。

hZkfFx.png

队列图解

hZAS1S.png

队列在程序中的应用

  • 打印队列：计算机打印多个文件的时候，需要排队打印。
  • 线程队列：当开启多线程时，当新开启的线程所需的资源不足时就先放入线程队列，等待 CPU 处理。

队列的实现

队列的实现和栈一样，有两种方案：

  • 基于数组实现。
  • 基于链表实现。

队列常见的操作

  • enqueue(element) 向队列尾部添加一个（或多个）新的项。
  • dequeue() 移除队列的第一（即排在队列最前面的）项，并返回被移除的元素。
  • front() 返回队列中的第一个元素——最先被添加，也将是最先被移除的元素。队列不做任何变动（不移除元素，只返回元素信息与 Map 类的 peek 方法非常类似）。
  • isEmpty() 如果队列中不包含任何元素，返回 true，否则返回 false。
  • size() 返回队列包含的元素个数，与数组的 length 属性类似。
  • toString() 将队列中的内容，转成字符串形式。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Queue {
  constructor() {
    this.items = [];
  }

  // enqueue(item) 入队，将元素加入到队列中
  enqueue(item) {
    this.items.push(item);
  }

  // dequeue() 出队，从队列中删除队头元素，返回删除的那个元素
  dequeue() {
    return this.items.shift();
  }

  // front() 查看队列的队头元素
  front() {
    return this.items[0];
  }

  // isEmpty() 查看队列是否为空
  isEmpty() {
    return this.items.length === 0;
  }

  // size() 查看队列中元素的个数
  size() {
    return this.items.length;
  }

  // toString() 将队列中的元素以字符串形式返回
  toString() {
    let result = "";
    for (let item of this.items) {
      result += item + " ";
    }
    return result;
  }
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
const queue = new Queue();

// enqueue() 测试
queue.enqueue("a");
queue.enqueue("b");
queue.enqueue("c");
queue.enqueue("d");
console.log(queue.items); //--> ["a", "b", "c", "d"]

// dequeue() 测试
queue.dequeue();
queue.dequeue();
console.log(queue.items); //--> ["c", "d"]

// front() 测试
console.log(queue.front()); //--> c

// isEmpty() 测试
console.log(queue.isEmpty()); //--> false

// size() 测试
console.log(queue.size()); //--> 2

// toString() 测试
console.log(queue.toString()); //--> c d

队列的应用

使用队列实现小游戏：击鼓传花。

分析：传入一组数据集合和设定的数字 number，循环遍历数组内元素，遍历到的元素为指定数字 number 时将该元素删除，直至数组剩下一个元素。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 利用队列结构的特点实现击鼓传花游戏求解方法的封装
function passGame(nameList, number) {
  // 1、new 一个 Queue 对象
  const queue = new Queue();

  // 2、将 nameList 里面的每一个元素入队
  for (const name of nameList) {
    queue.enqueue(name);
  }

  // 3、开始数数
  // 队列中只剩下 1 个元素时就停止数数
  while (queue.size() > 1) {
    // 不是 number 时，重新加入到队尾
    // 是 number 时，将其删除

    for (let i = 0; i < number - 1; i++) {
      // number 数字之前的人重新放入到队尾（即把队头删除的元素，重新加入到队列中）
      queue.enqueue(queue.dequeue());
    }

    // number 对应这个人，直接从队列中删除
    // 由于队列没有像数组一样的下标值不能直接取到某一元素，
    // 所以采用，把 number 前面的 number - 1 个元素先删除后添加到队列末尾，
    // 这样第 number 个元素就排到了队列的最前面，可以直接使用 dequeue 方法进行删除
    queue.dequeue();
  }

  // 4、获取最后剩下的那个人
  const endName = queue.front();

  // 5、返回这个人在原数组中对应的索引
  return nameList.indexOf(endName);
}

测试代码

1
2
3
4
// passGame() 测试
const names = ["lily", "lucy", "tom", "tony", "jack"];
const targetIndex = passGame(names, 4);
console.log("击鼓传花", names[targetIndex]); //--> lily

优先队列

场景

生活中类似优先队列的场景：

  • 优先排队的人，优先处理。 (买票、结账、WC)。
  • 排队中，有紧急情况（特殊情况）的人可优先处理。

优先队列

优先级队列主要考虑的问题：

  • 每个元素不再只是一个数据，还包含优先级。
  • 在添加元素过程中，根据优先级放入到正确位置。

优先队列的实现

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
// 优先队列内部的元素类
class QueueElement {
  constructor(element, priority) {
    this.element = element;
    this.priority = priority;
  }
}

// 优先队列类（继承 Queue 类）
export class PriorityQueue extends Queue {
  constructor() {
    super();
  }

  // enqueue(element, priority) 入队，将元素按优先级加入到队列中
  // 重写 enqueue()
  enqueue(element, priority) {
    // 根据传入的元素，创建 QueueElement 对象
    const queueElement = new QueueElement(element, priority);

    // 判断队列是否为空
    if (this.isEmpty()) {
      // 如果为空，不用判断优先级，直接添加
      this.items.push(queueElement);
    } else {
      // 定义一个变量记录是否成功添加了新元素
      let added = false;

      for (let i = 0; i < this.items.length; i++) {
        // 让新插入的元素进行优先级比较，priority 值越小，优先级越大
        if (queueElement.priority < this.items[i].priority) {
          // 在指定的位置插入元素
          this.items.splice(i, 0, queueElement);
          added = true;
          break;
        }
      }

      // 如果遍历完所有元素，优先级都大于新插入的元素，就将新插入的元素插入到最后
      if (!added) {
        this.items.push(queueElement);
      }
    }
  }

  // dequeue() 出队，从队列中删除前端元素，返回删除的元素
  // 继承 Queue 类的 dequeue()
  dequeue() {
    return super.dequeue();
  }

  // front() 查看队列的前端元素
  // 继承 Queue 类的 front()
  front() {
    return super.front();
  }

  // isEmpty() 查看队列是否为空
  // 继承 Queue 类的 isEmpty()
  isEmpty() {
    return super.isEmpty();
  }

  // size() 查看队列中元素的个数
  // 继承 Queue 类的 size()
  size() {
    return super.size();
  }

  // toString() 将队列中元素以字符串形式返回
  // 重写 toString()
  toString() {
    let result = "";
    for (let item of this.items) {
      result += item.element + "-" + item.priority + " ";
    }
    return result;
  }
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
const priorityQueue = new PriorityQueue();

// 入队 enqueue() 测试
priorityQueue.enqueue("A", 10);
priorityQueue.enqueue("B", 15);
priorityQueue.enqueue("C", 11);
priorityQueue.enqueue("D", 20);
priorityQueue.enqueue("E", 18);
console.log(priorityQueue.items);
//--> output:
// QueueElement {element: "A", priority: 10}
// QueueElement {element: "C", priority: 11}
// QueueElement {element: "B", priority: 15}
// QueueElement {element: "E", priority: 18}
// QueueElement {element: "D", priority: 20}

// 出队 dequeue() 测试
priorityQueue.dequeue();
priorityQueue.dequeue();
console.log(priorityQueue.items);
//--> output:
// QueueElement {element: "B", priority: 15}
// QueueElement {element: "E", priority: 18}
// QueueElement {element: "D", priority: 20}

// isEmpty() 测试
console.log(priorityQueue.isEmpty()); //--> false

// size() 测试
console.log(priorityQueue.size()); //--> 3

// toString() 测试
console.log(priorityQueue.toString()); //--> B-15 E-18 D-20

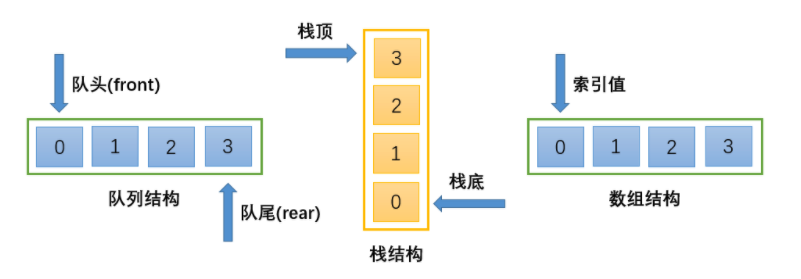
数组、栈和队列图解

hZAXDJ.png

单向链表

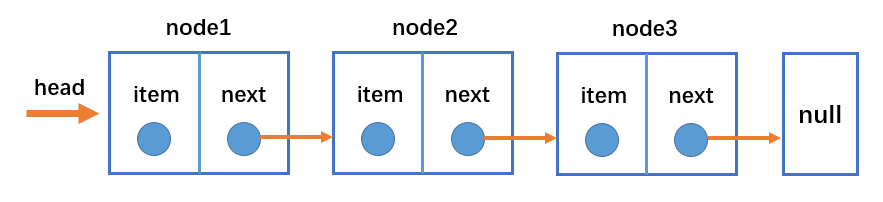
认识链表

链表和数组

链表和数组一样，可以用于存储一系列的元素，但是链表和数组的实现机制完全不同。

数组

  • 存储多个元素，数组（或列表）可能是最常用的数据结构。

  • 几乎每一种编程语言都有默认实现数组结构，提供了一个便利的 [] 语法来访问数组元素。

  • 数组缺点：

    数组的创建需要申请一段连续的内存空间(一整块内存)，并且大小是固定的，当前数组不能满足容量需求时，需要扩容。 (一般情况下是申请一个更大的数组，比如 2 倍，然后将原数组中的元素复制过去)

    在数组开头或中间位置插入数据的成本很高，需要进行大量元素的位移。

链表

  • 存储多个元素，另外一个选择就是使用链表。

  • 不同于数组，链表中的元素在内存中不必是连续的空间。

  • 链表的每个元素由一个存储元素本身的节点和一个指向下一个元素的引用(有些语言称为指针)组成。

  • 链表优点：

    内存空间不必是连续的，可以充分利用计算机的内存，实现灵活的内存动态管理。

    链表不必在创建时就确定大小，并且大小可以无限延伸下去。

    链表在插入和删除数据时，时间复杂度可以达到 O(1)，相对数组效率高很多。

  • 链表缺点：

    访问任何一个位置的元素时，需要从头开始访问。(无法跳过第一个元素访问任何一个元素)

    无法通过下标值直接访问元素，需要从头开始一个个访问，直到找到对应的元素。

    虽然可以轻松地到达下一个节点，但是回到前一个节点是很难的。

单向链表

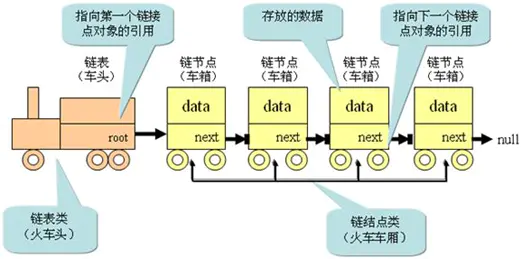
单向链表类似于火车，有一个火车头，火车头会连接一个节点，节点上有乘客，并且这个节点会连接下一个节点，以此类推。

  • 链表的火车结构

    hZEBMF.png

  • 链表的数据结构

    head 属性指向链表的第一个节点。
    链表中的最后一个节点指向 null。
    当链表中一个节点也没有的时候，head 直接指向 null。

hZEDr4.png

  • 给火车加上数据后的结构

    hZErqJ.png

链表中的常见操作

  • append(element) 向链表尾部添加一个新的项。
  • insert(position, element) 向链表的特定位置插入一个新的项。
  • get(position) 获取对应位置的元素。
  • indexOf(element) 返回元素在链表中的索引。如果链表中没有该元素就返回-1。
  • update(position, element) 修改某个位置的元素。
  • removeAt(position) 从链表的特定位置移除一项。
  • remove(element) 从链表中移除一项。
  • isEmpty() 如果链表中不包含任何元素，返回 true，如果链表长度大于 0 则返回 false。
  • size() 返回链表包含的元素个数，与数组的 length 属性类似。
  • toString() 由于链表项使用了 Node 类，就需要重写继承自 JavaScript 对象默认的 toString 方法，让其只输出元素的值。

单向链表的封装

创建单向链表类

先创建单向链表类 LinkedList，添加基本属性，再逐步实现单向链表的常用方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class LinkedList {
  // 初始链表长度为 0
  length = 0;

  // 初始 head 为 null，head 指向链表的第一个节点
  head = null;

  // 内部类（链表里的节点 Node）
  Node = class {
    data;
    next = null;
    constructor(data) {
      this.data = data;
    }
  };
}

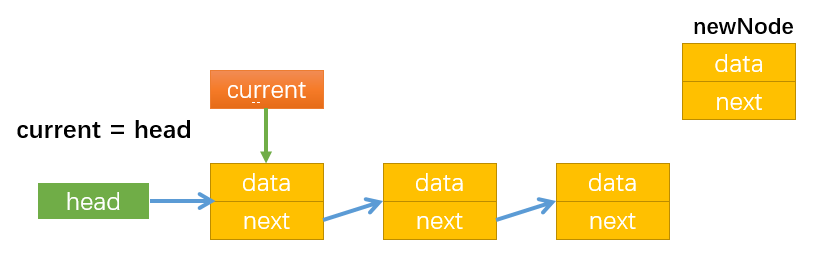
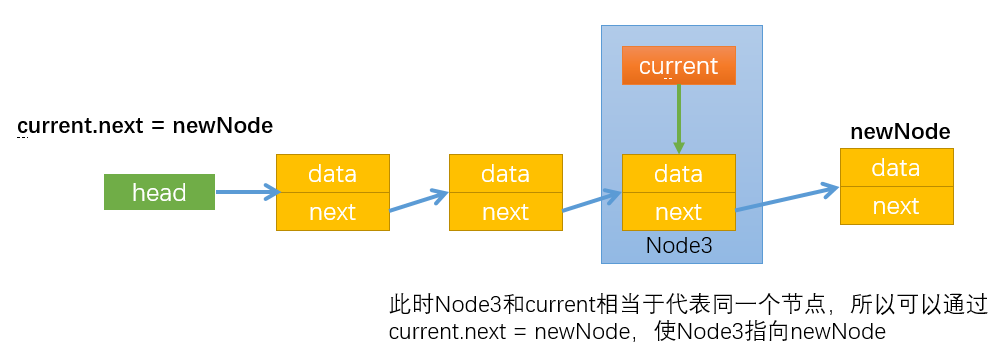
实现 append() 方法

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// append() 往链表尾部追加数据
append(data) {

    // 1、创建新节点
    const newNode = new this.Node(data);

    // 2、追加新节点
    if (this.length === 0) {

    // 链表长度为 0 时，即只有 head 的时候
    this.head = newNode;

    } else {
    // 链表长度大于 0 时，在最后面添加新节点
    let currentNode = this.head;

    // 当 currentNode.next 不为空时，
    // 循序依次找最后一个节点，即节点的 next 为 null 时
    while (currentNode.next !== null) {
        currentNode = currentNode.next;
    }

    // 最后一个节点的 next 指向新节点
    currentNode.next = newNode;
    }

    // 3、追加完新节点后，链表长度 + 1
    this.length++;

}
过程图解

  • 首先让 currentNode 指向第一个节点。

    image

  • 通过 while 循环使 currentNode 指向最后一个节点，最后通过 currentNode.next = newNode，让最后一个节点指向新节点 newNode。

    image

代码测试
1
2
3
4
5
6
const linkedList = new LinkedList();
// 测试 append 方法
linkedList.append("A");
linkedList.append("B");
linkedList.append("C");
console.log(linkedList);

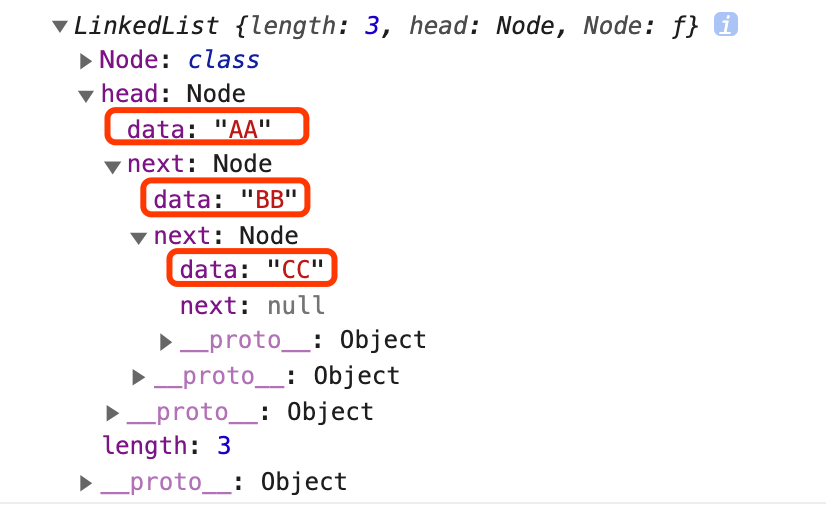
image

实现 toString() 方法

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
toString() {
    let currentNode = this.head;
    let result = '';

    // 遍历所有的节点，拼接为字符串，直到节点为 null
    while (currentNode) {
    result += currentNode.data + ' ';
    currentNode = currentNode.next;
    }

    return result;
}
代码测试
1
2
// 测试 toString 方法
console.log(linkedList.toString()); //--> AA BB CC

实现 insert() 方法

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// insert() 在指定位置（position）插入节点
insert(position, data) {
    // position 新插入节点的位置
    // position = 0 表示新插入后是第一个节点
    // position = 1 表示新插入后是第二个节点，以此类推

    // 1、对 position 进行越界判断，不能小于 0 或大于链表长度
    if (position < 0 || position > this.length) return false;

    // 2、创建新节点
    const newNode = new this.Node(data);

    // 3、插入节点
    if (position === 0) { // position = 0 的情况
    // 让新节点的 next 指向 原来的第一个节点，即 head
    newNode.next = this.head;

    // head 赋值为 newNode
    this.head = newNode;
    } else { // 0 < position <= length 的情况

    // 初始化一些变量
    let currentNode = this.head; // 当前节点初始化为 head
    let previousNode = null; // head 的 上一节点为 null
    let index = 0; // head 的 index 为 0

    // 在 0 ~ position 之间遍历，不断地更新 currentNode 和 previousNode
    // 直到找到要插入的位置
    while (index++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
    }

    // 在当前节点和当前节点的上一节点之间插入新节点，即它们的改变指向
    newNode.next = currentNode;
    previousNode.next = newNode;
    }

    // 更新链表长度
    this.length++;
    return newNode;
}
代码测试
1
2
3
4
// 测试 insert 方法
linkedList.insert(0, "123");
linkedList.insert(2, "456");
console.log(linkedList.toString()); //--> 123 AA 456 BB CC

实现 getData() 方法

获取指定位置（position）的 data。

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
getData(position) {
    // 1、position 越界判断
    if (position < 0 || position >= this.length) return null;

    // 2、获取指定 position 节点的 data
    let currentNode = this.head;
    let index = 0;

    while (index++ < position) {
    currentNode = currentNode.next;
    }
    // 3、返回 data
    return currentNode.data;
}
代码测试
1
2
3
// 测试 getData 方法
console.log(linkedList.getData(0)); //--> 123
console.log(linkedList.getData(1)); //--> AA

实现 indexOf() 方法

indexOf(data) 返回指定 data 的 index，如果没有，返回 -1。

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
indexOf(data) {

    let currentNode = this.head;
    let index = 0;

    while (currentNode) {
    if (currentNode.data === data) {
        return index;
    }
    currentNode = currentNode.next;
    index++;
    }

    return -1;
}
代码测试
1
2
3
// 测试 indexOf 方法
console.log(linkedList.indexOf("AA")); //--> 1
console.log(linkedList.indexOf("ABC")); //--> -1

实现 update() 方法

update(position, data) 修改指定位置节点的 data。

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
update(position, data) {
    // 涉及到 position 都要进行越界判断
    // 1、position 越界判断
    if (position < 0 || position >= this.length) return false;

    // 2、痛过循环遍历，找到指定 position 的节点
    let currentNode = this.head;
    let index = 0;
    while (index++ < position) {
    currentNode = currentNode.next;
    }

    // 3、修改节点 data
    currentNode.data = data;

    return currentNode;
}
代码测试
1
2
3
4
5
// 测试 update 方法
linkedList.update(0, "12345");
console.log(linkedList.toString()); //--> 12345 AA 456 BB CC
linkedList.update(1, "54321");
console.log(linkedList.toString()); //--> 12345 54321 456 BB CC

实现 removeAt() 方法

removeAt(position) 删除指定位置的节点。

代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
removeAt(position) {
    // 1、position 越界判断
    if (position < 0 || position >= this.length) return null;

    // 2、删除指定 position 节点
    let currentNode = this.head;
    if (position === 0) {
    // position = 0 的情况
    this.head = this.head.next;

    } else {
    // position > 0 的情况
    // 通过循环遍历，找到指定 position 的节点，赋值到 currentNode

    let previousNode = null;
    let index = 0;

    while (index++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
    }

    // 巧妙之处，让上一节点的 next 指向到当前的节点的 next，相当于删除了当前节点。
    previousNode.next = currentNode.next;
    }

    // 3、更新链表长度 -1
    this.length--;

    return currentNode;
}
代码测试
1
2
3
// 测试 removeAt 方法
linkedList.removeAt(3);
console.log(linkedList.toString()); //--> 12345 54321 456 CC

实现 remove() 方法

remove(data) 删除指定 data 所在的节点。

代码实现
1
2
3
remove(data) {
    this.removeAt(this.indexOf(data));
}
代码测试
1
2
3
// 测试 remove 方法
linkedList.remove("CC");
console.log(linkedList.toString()); //--> 12345 54321 456

实现 isEmpty() 方法

isEmpty() 判断链表是否为空。

代码实现
1
2
3
isEmpty() {
    return this.length === 0;
}
代码测试
1
2
// 测试 isEmpty 方法
console.log(linkedList.isEmpty()); //--> false

实现 size() 方法

size() 获取链表的长度。

代码实现
1
2
3
size() {
    return this.length;
}
代码测试
1
2
// 测试 size 方法
console.log(linkedList.size()); //--> 3

完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
class LinkedList {
  // 初始链表长度为 0
  length = 0;

  // 初始 head 为 null，head 指向链表的第一个节点
  head = null;

  // 内部类（链表里的节点 Node）
  Node = class {
    data;
    next = null;

    constructor(data) {
      this.data = data;
    }
  };

  // ------------ 链表的常见操作 ------------ //

  // append() 往链表尾部追加数据
  append(data) {
    // 1、创建新节点
    const newNode = new this.Node(data);

    // 2、追加新节点
    if (this.length === 0) {
      // 链表长度为 0 时，即只有 head 的时候
      this.head = newNode;
    } else {
      // 链表长度大于 0 时，在最后面添加新节点
      let currentNode = this.head;

      // 当 currentNode.next 不为空时，
      // 循序依次找最后一个节点，即节点的 next 为 null 时
      while (currentNode.next !== null) {
        currentNode = currentNode.next;
      }

      // 最后一个节点的 next 指向新节点
      currentNode.next = newNode;
    }

    // 3、追加完新节点后，链表长度 + 1
    this.length++;
  }

  // insert() 在指定位置（position）插入节点
  insert(position, data) {
    // position 新插入节点的位置
    // position = 0 表示新插入后是第一个节点
    // position = 1 表示新插入后是第二个节点，以此类推

    // 1、对 position 进行越界判断，不能小于 0 或大于链表长度
    if (position < 0 || position > this.length) return false;

    // 2、创建新节点
    const newNode = new this.Node(data);

    // 3、插入节点
    if (position === 0) {
      // position = 0 的情况
      // 让新节点的 next 指向 原来的第一个节点，即 head
      newNode.next = this.head;

      // head 赋值为 newNode
      this.head = newNode;
    } else {
      // 0 < position <= length 的情况

      // 初始化一些变量
      let currentNode = this.head; // 当前节点初始化为 head
      let previousNode = null; // head 的 上一节点为 null
      let index = 0; // head 的 index 为 0

      // 在 0 ~ position 之间遍历，不断地更新 currentNode 和 previousNode
      // 直到找到要插入的位置
      while (index++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
      }

      // 在当前节点和当前节点的上一节点之间插入新节点，即它们的改变指向
      newNode.next = currentNode;
      previousNode.next = newNode;
    }

    // 更新链表长度
    this.length++;
    return newNode;
  }

  // getData() 获取指定位置的 data
  getData(position) {
    // 1、position 越界判断
    if (position < 0 || position >= this.length) return null;

    // 2、获取指定 position 节点的 data
    let currentNode = this.head;
    let index = 0;

    while (index++ < position) {
      currentNode = currentNode.next;
    }

    // 3、返回 data
    return currentNode.data;
  }

  // indexOf() 返回指定 data 的 index，如果没有，返回 -1。
  indexOf(data) {
    let currentNode = this.head;
    let index = 0;

    while (currentNode) {
      if (currentNode.data === data) {
        return index;
      }
      currentNode = currentNode.next;
      index++;
    }

    return -1;
  }

  // update() 修改指定位置节点的 data
  update(position, data) {
    // 涉及到 position 都要进行越界判断
    // 1、position 越界判断
    if (position < 0 || position >= this.length) return false;

    // 2、痛过循环遍历，找到指定 position 的节点
    let currentNode = this.head;
    let index = 0;
    while (index++ < position) {
      currentNode = currentNode.next;
    }

    // 3、修改节点 data
    currentNode.data = data;

    return currentNode;
  }

  // removeAt() 删除指定位置的节点
  removeAt(position) {
    // 1、position 越界判断
    if (position < 0 || position >= this.length) return null;

    // 2、删除指定 position 节点
    let currentNode = this.head;
    if (position === 0) {
      // position = 0 的情况
      this.head = this.head.next;
    } else {
      // position > 0 的情况
      // 通过循环遍历，找到指定 position 的节点，赋值到 currentNode

      let previousNode = null;
      let index = 0;

      while (index++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
      }

      // 巧妙之处，让上一节点的 next 指向到当前的节点的 next，相当于删除了当前节点。
      previousNode.next = currentNode.next;
    }

    // 3、更新链表长度 -1
    this.length--;

    return currentNode;
  }

  // remove() 删除指定 data 的节点
  remove(data) {
    this.removeAt(this.indexOf(data));
  }

  // isEmpty() 判断链表是否为空
  isEmpty() {
    return this.length === 0;
  }

  // size() 获取链表的长度
  size() {
    return this.length;
  }

  // toString() 链表数据以字符串形式返回
  toString() {
    let currentNode = this.head;
    let result = "";

    // 遍历所有的节点，拼接为字符串，直到节点为 null
    while (currentNode) {
      result += currentNode.data + " ";
      currentNode = currentNode.next;
    }

    return result;
  }
}

双向链表

单向链表和双向链表

单向链表

  • 只能从头遍历到尾或者从尾遍历到头（一般从头到尾）。
  • 链表相连的过程是单向的，实现原理是上一个节点中有指向下一个节点的引用。
  • 单向链表有一个比较明显的缺点：可以轻松到达下一个节点，但回到前一个节点很难，在实际开发中, 经常会遇到需要回到上一个节点的情况。

双向链表

  • 既可以从头遍历到尾，也可以从尾遍历到头。
  • 链表相连的过程是双向的。实现原理是一个节点既有向前连接的引用，也有一个向后连接的引用。
  • 双向链表可以有效的解决单向链表存在的问题。
  • 双向链表缺点：
    • 每次在插入或删除某个节点时，都需要处理四个引用，而不是两个，实现起来会困难些。
    • 相对于单向链表，所占内存空间更大一些。
    • 但是，相对于双向链表的便利性而言，这些缺点微不足道。

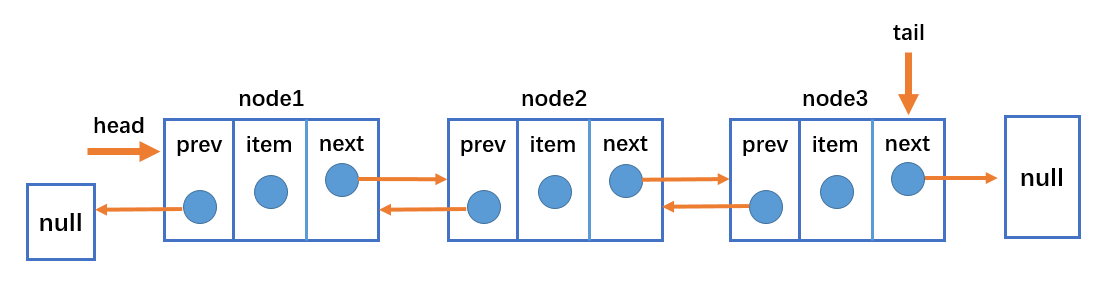
双向链表结构

hZZ2jO.png

  • 双向链表不仅有 head 指针指向第一个节点，而且有 tail 指针指向最后一个节点。
  • 每一个节点由三部分组成：item 储存数据、prev 指向前一个节点、next 指向后一个节点。
  • 双向链表的第一个节点的 prev 指向 null。
  • 双向链表的最后一个节点的 next 指向 null。

双向链表常见的操作

  • append(element) 向链表尾部追加一个新元素。
  • insert(position, element) 向链表的指定位置插入一个新元素。
  • getElement(position) 获取指定位置的元素。
  • indexOf(element) 返回元素在链表中的索引。如果链表中没有该元素就返回 -1。
  • update(position, element) 修改指定位置上的元素。
  • removeAt(position) 从链表中的删除指定位置的元素。
  • remove(element) 从链表删除指定的元素。
  • isEmpty() 如果链表中不包含任何元素，返回 trun，如果链表长度大于 0 则返回 false。
  • size() 返回链表包含的元素个数，与数组的 length 属性类似。
  • toString() 由于链表项使用了 Node 类，就需要重写继承自 JavaScript 对象默认的 toString 方法，让其只输出元素的值。
  • forwardString() 返回正向遍历节点字符串形式。
  • backwordString() 返回反向遍历的节点的字符串形式。

双向链表的封装

创建双向链表类 DoublyLinkedList

  • DoublyNode 类继承单向链表的 Node 类，新添加 this.prev 属性，该属性用于指向上一个节点。
  • DoublyLinkedList 类继承 LinkedList 类，新添加 this.tail 属性，该属性指向末尾的节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 双向链表的节点类（继承单向链表的节点类）
class DoublyNode extends Node {
  constructor(element) {
    super(element);
    this.prev = null;
  }
}

// 双向链表类继承单向链表类
class DoublyLinkedList extends LinkedList {
  constructor() {
    super();
    this.tail = null;
  }
}

append(element)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// append(element) 往双向链表尾部追加一个新的元素
// 重写 append()
append(element) {

// 1、创建双向链表节点
const newNode = new DoublyNode(element);

// 2、追加元素
if (this.head === null) {
  this.head = newNode;
  this.tail = newNode;
} else {
  // ！！跟单向链表不同，不用通过循环找到最后一个节点
  // 巧妙之处
  this.tail.next = newNode;
  newNode.prev = this.tail;
  this.tail = newNode;
}

this.length++;
}

insert(position, element)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// insert(position, data) 插入元素
// 重写 insert()
insert(position, element) {
    // 1、position 越界判断
    if (position < 0 || position > this.length) return false;

    // 2、创建新的双向链表节点
    const newNode = new DoublyNode(element);

    // 3、判断多种插入情况
    if (position === 0) { // 在第 0 个位置插入

      if (this.head === null) {
        this.head = newNode;
        this.tail = newNode;
      } else {
        //== 巧妙之处：相处腾出 this.head 空间，留个 newNode 来赋值 ==//
        newNode.next = this.head;
        this.head.perv = newNode;
        this.head = newNode;
      }

    } else if (position === this.length) { // 在最后一个位置插入

      this.tail.next = newNode;
      newNode.prev = this.tail;
      this.tail = newNode;
    } else { // 在 0 ~ this.length 位置中间插入

      let targetIndex = 0;
      let currentNode = this.head;
      let previousNode = null;

      // 找到要插入位置的节点
      while (targetIndex++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
      }

      // 交换节点信息
      previousNode.next = newNode;
      newNode.prev = previousNode;

      newNode.next = currentNode;
      currentNode.prev = newNode;
    }

    this.length++;

    return true;
  }

insert(position, element)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// insert(position, data) 插入元素
// 重写 insert()
  insert(position, element) {
    // 1、position 越界判断
    if (position < 0 || position > this.length) return false;

    // 2、创建新的双向链表节点
    const newNode = new DoublyNode(element);

    // 3、判断多种插入情况
    if (position === 0) { // 在第 0 个位置插入

      if (this.head === null) {
        this.head = newNode;
        this.tail = newNode;
      } else {
        //== 巧妙之处：相处腾出 this.head 空间，留个 newNode 来赋值 ==//
        newNode.next = this.head;
        this.head.perv = newNode;
        this.head = newNode;
      }

    } else if (position === this.length) { // 在最后一个位置插入

      this.tail.next = newNode;
      newNode.prev = this.tail;
      this.tail = newNode;
    } else { // 在 0 ~ this.length 位置中间插入

      let targetIndex = 0;
      let currentNode = this.head;
      let previousNode = null;

      // 找到要插入位置的节点
      while (targetIndex++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
      }

      // 交换节点信息
      previousNode.next = newNode;
      newNode.prev = previousNode;

      newNode.next = currentNode;
      currentNode.prev = newNode;
    }

    this.length++;

    return true;
  }

removeAt(position)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// removeAt() 删除指定位置的节点
// 重写 removeAt()
removeAt(position) {
  // 1、position 越界判断
  if (position < 0 || position > this.length - 1) return null;

  // 2、根据不同情况删除元素
  let currentNode = this.head;
  if (position === 0) { // 删除第一个节点的情况

    if (this.length === 1) { // 链表内只有一个节点的情况
      this.head = null;
      this.tail = null;
    } else { // 链表内有多个节点的情况
      this.head = this.head.next;
      this.head.prev = null;
    }

  } else if (position === this.length - 1) { // 删除最后一个节点的情况

    currentNode = this.tail;
    this.tail.prev.next = null;
    this.tail = this.tail.prev;

  } else { // 删除 0 ~ this.length - 1 里面节点的情况

    let targetIndex = 0;
    let previousNode = null;
    while (targetIndex++ < position) {
      previousNode = currentNode;
      currentNode = currentNode.next;
    }

    previousNode.next = currentNode.next;
    currentNode.next.perv = previousNode;

  }

  this.length--;
  return currentNode.data;
}

update(position, data)

1
2
3
4
5
6
7
8
9
10
// update(position, data) 修改指定位置的节点
// 重写 update()
update(position, data) {
  // 1、删除 position 位置的节点
  const result = this.removeAt(position);

  // 2、在 position 位置插入元素
  this.insert(position, data);
  return result;
}

forwardToString()

1
2
3
4
5
6
7
8
9
10
11
12
13
// forwardToString() 链表数据从前往后以字符串形式返回
  forwardToString() {
    let currentNode = this.head;
    let result = '';

    // 遍历所有的节点，拼接为字符串，直到节点为 null
    while (currentNode) {
      result += currentNode.data + '--';
      currentNode = currentNode.next;
    }

    return result;
  }

backwardString()

1
2
3
4
5
6
7
8
9
10
11
12
13
// backwardString() 链表数据从后往前以字符串形式返回
  backwardString() {
    let currentNode = this.tail;
    let result = '';

    // 遍历所有的节点，拼接为字符串，直到节点为 null
    while (currentNode) {
      result += currentNode.data + '--';
      currentNode = currentNode.prev;
    }

    return result;
  }

其他方法的实现

双向链表的其他方法通过继承单向链表来实现。

完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
class DoublyLinkedList extends LinkedList {
  constructor() {
    super();
    this.tail = null;
  }

  // ------------ 链表的常见操作 ------------ //
  // append(element) 往双向链表尾部追加一个新的元素
  // 重写 append()
  append(element) {
    // 1、创建双向链表节点
    const newNode = new DoublyNode(element);

    // 2、追加元素
    if (this.head === null) {
      this.head = newNode;
      this.tail = newNode;
    } else {
      // ！！跟单向链表不同，不用通过循环找到最后一个节点
      // 巧妙之处
      this.tail.next = newNode;
      newNode.prev = this.tail;
      this.tail = newNode;
    }

    this.length++;
  }

  // insert(position, data) 插入元素
  // 重写 insert()
  insert(position, element) {
    // 1、position 越界判断
    if (position < 0 || position > this.length) return false;

    // 2、创建新的双向链表节点
    const newNode = new DoublyNode(element);

    // 3、判断多种插入情况
    if (position === 0) {
      // 在第 0 个位置插入

      if (this.head === null) {
        this.head = newNode;
        this.tail = newNode;
      } else {
        //== 巧妙之处：相处腾出 this.head 空间，留个 newNode 来赋值 ==//
        newNode.next = this.head;
        this.head.perv = newNode;
        this.head = newNode;
      }
    } else if (position === this.length) {
      // 在最后一个位置插入

      this.tail.next = newNode;
      newNode.prev = this.tail;
      this.tail = newNode;
    } else {
      // 在 0 ~ this.length 位置中间插入

      let targetIndex = 0;
      let currentNode = this.head;
      let previousNode = null;

      // 找到要插入位置的节点
      while (targetIndex++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
      }

      // 交换节点信息
      previousNode.next = newNode;
      newNode.prev = previousNode;

      newNode.next = currentNode;
      currentNode.prev = newNode;
    }

    this.length++;

    return true;
  }

  // getData() 继承单向链表
  getData(position) {
    return super.getData(position);
  }

  // indexOf() 继承单向链表
  indexOf(data) {
    return super.indexOf(data);
  }

  // removeAt() 删除指定位置的节点
  // 重写 removeAt()
  removeAt(position) {
    // 1、position 越界判断
    if (position < 0 || position > this.length - 1) return null;

    // 2、根据不同情况删除元素
    let currentNode = this.head;
    if (position === 0) {
      // 删除第一个节点的情况

      if (this.length === 1) {
        // 链表内只有一个节点的情况
        this.head = null;
        this.tail = null;
      } else {
        // 链表内有多个节点的情况
        this.head = this.head.next;
        this.head.prev = null;
      }
    } else if (position === this.length - 1) {
      // 删除最后一个节点的情况

      currentNode = this.tail;
      this.tail.prev.next = null;
      this.tail = this.tail.prev;
    } else {
      // 删除 0 ~ this.length - 1 里面节点的情况

      let targetIndex = 0;
      let previousNode = null;
      while (targetIndex++ < position) {
        previousNode = currentNode;
        currentNode = currentNode.next;
      }

      previousNode.next = currentNode.next;
      currentNode.next.perv = previousNode;
    }

    this.length--;
    return currentNode.data;
  }

  // update(position, data) 修改指定位置的节点
  // 重写 update()
  update(position, data) {
    // 1、删除 position 位置的节点
    const result = this.removeAt(position);

    // 2、在 position 位置插入元素
    this.insert(position, data);
    return result;
  }

  // remove(data) 删除指定 data 所在的节点（继承单向链表）
  remove(data) {
    return super.remove(data);
  }

  // isEmpty() 判断链表是否为空
  isEmpty() {
    return super.isEmpty();
  }

  // size() 获取链表的长度
  size() {
    return super.size();
  }

  // forwardToString() 链表数据从前往后以字符串形式返回
  forwardToString() {
    let currentNode = this.head;
    let result = "";

    // 遍历所有的节点，拼接为字符串，直到节点为 null
    while (currentNode) {
      result += currentNode.data + "--";
      currentNode = currentNode.next;
    }

    return result;
  }

  // backwardString() 链表数据从后往前以字符串形式返回
  backwardString() {
    let currentNode = this.tail;
    let result = "";

    // 遍历所有的节点，拼接为字符串，直到节点为 null
    while (currentNode) {
      result += currentNode.data + "--";
      currentNode = currentNode.prev;
    }

    return result;
  }
}

代码测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
const doublyLinkedList = new DoublyLinkedList();

// append() 测试
doublyLinkedList.append("ZZ");
doublyLinkedList.append("XX");
doublyLinkedList.append("CC");
console.log(doublyLinkedList);

// insert() 测试
doublyLinkedList.insert(0, "00");
doublyLinkedList.insert(2, "22");
console.log(doublyLinkedList);

// getData() 测试
console.log(doublyLinkedList.getData(1)); //--> ZZ

// indexOf() 测试
console.log(doublyLinkedList.indexOf("XX")); //--> 3
console.log(doublyLinkedList);

// removeAt() 测试
doublyLinkedList.removeAt(0);
doublyLinkedList.removeAt(1);
console.log(doublyLinkedList);

// update() 测试
doublyLinkedList.update(0, "111111");
console.log(doublyLinkedList);

// remove() 测试
console.log(doublyLinkedList.remove("111111"));
console.log(doublyLinkedList.remove("22222"));
console.log(doublyLinkedList);

// forwardToString() 测试
console.log(doublyLinkedList.forwardToString());

// backwardString() 测试
console.log(doublyLinkedList.backwardString());

集合

集合

几乎每种编程语言中，都有集合结构。集合比较常见的实现方式是哈希表，这里使用 JavaScript 的 Object 进行封装。

集合特点

  • 集合通常是由一组无序的、不能重复的元素构成。

  • 数学中常指的集合中的元素是可以重复的，但是计算机中集合的元素不能重复。

  • 集合是特殊的数组。

    • 特殊之处在于里面的元素没有顺序，也不能重复。
    • 没有顺序意味着不能通过下标值进行访问，不能重复意味着相同的对象在集合中只会存在一份。

封装集合

ES6 中的 Set 就是一个集合类，这里我们重新封装一个 Set 类，了解集合的底层实现。

集合常见的操作

  • add(value) 向集合添加一个新的项。
  • remove(value) 从集合移除一个值。
  • has(value) 如果值在集合中，返回 true，否则返回false。
  • clear() 移除集合中的所有项。
  • size() 返回集合所包含元素的数量。与数组的 length 属性类似。
  • values() 返回一个包含集合中所有值的数组。
  • 还有其他的方法，用的不多，这里不做封装。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// 集合结构的封装
class Set {
  constructor() {
    this.items = {};
  }

  // has(value) 判断集合中是否存在 value 值，存在返回 true，否则返回 false
  has(value) {
    return this.items.hasOwnProperty(value);
  }

  // add(value) 往集合中添加 value
  add(value) {
    if (this.has(value)) return false;
    this.items[value] = value;
    return true;
  }

  // remove(value) 删除集合中指定的 value
  remove(value) {
    // 如果集合不存在该 value，返回 false
    if (!this.has(value)) return false;
    delete this.items[value];
  }

  // clear() 清空集合中所有 value
  clear() {
    this.items = {};
  }

  // size() 获取集合中的 value 个数
  size() {
    return Object.keys(this.items).length;
  }

  // values() 获取集合中所有的 value
  values() {
    return Object.keys(this.items);
  }
}

代码测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
const set = new Set();

// add() 测试
set.add("abc");
set.add("abc");
set.add("123");
set.add("zxc");
console.log(set); //--> {items: {123: "123", abc: "abc", zxc: "zxc"}}

// has() 测试
console.log(set.has("123")); //--> true
console.log(set.has("456")); //--> false

// remove() 测试
set.remove("abc");
console.log(set); //--> {items: {123: "123", zxc: "zxc"}}

// size() 测试
console.log(set.size()); //--> 2

// values() 测试
console.log(set.values()); //--> ["123", "zxc"]

// clear() 测试
set.clear();
console.log(set.values()); //--> []

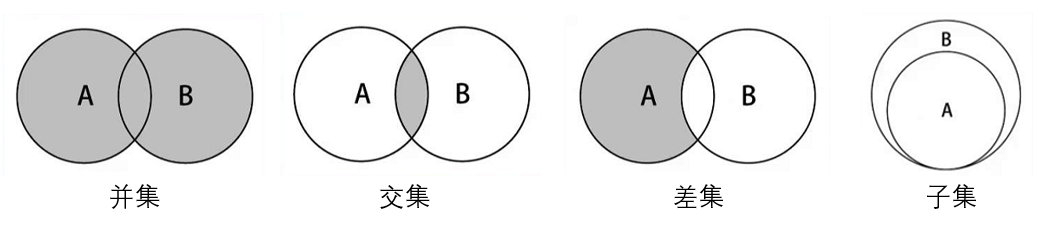
集合间的操作

  • 并集：对于给定的两个集合，返回一个包含两个集合中所有元素的新集合。
  • 交集：对于给定的两个集合，返回一个包含两个集合中共有元素的新集合。
  • 差集：对于给定的两个集合，返回一个包含所有存在于第一个集合且不存在于第二个集合的元素的新集合。
  • 子集：验证一个给定集合是否是另一个集合的子集。

hZem5R.png

并集的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// union() 求两个集合的并集
union(otherSet) {
    // 1、创建一个新集合
    let unionSet = new Set();

    // 2、将当前集合（this）的所有 value，添加到新集合（unionSet）中
    for (let value of this.values()) {
        unionSet.add(value);
    }

    // 3、将 otherSet 集合的所有 value，添加到新集合（unionSet）中
    for (let value of otherSet.values()) {
        unionSet.add(value); // add() 已经有重复判断
    }

    return unionSet;
}

交集的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// intersection() 求两个集合的交集
intersection(otherSet) {

    // 1、创建一个新集合
    let intersectionSet = new Set();

    // 2、从当前集合中取出每一个 value，判断是否在 otherSet 集合中存在
    for (let value of this.values()) {
        if (otherSet.has(value)) {
            intersectionSet.add(value);
        }
    }

    return intersectionSet;
}

差集的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// difference() 差集
difference(otherSet) {

    // 1、创建一个新集合
    let differenceSet = new Set();

    // 2、从当前集合中取出每一个 value，判断是否在 otherSet 集合中存在，不存在的即为差集
    for (let value of this.values()) {
        if (!otherSet.has(value)) {
            differenceSet.add(value);
        }
    }

    return differenceSet;
}

子集的实现

1
2
3
4
5
6
7
8
9
10
11
12
// subset() 子集
subset(otherSet) {

    // 从当前集合中取出每一个 value，判断是否在 otherSet 集合中存在，有不存在的返回 false
    // 遍历完所有的，返回 true
    for (let value of this.values()) {
        if (!otherSet.has(value)) {
            return false;
        }
    }
    return true;
}

集合的完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
// 集合结构的封装
export default class Set {
  constructor() {
    this.items = {};
  }

  // has(value) 判断集合中是否存在 value 值，存在返回 true，否则返回 false
  has(value) {
    return this.items.hasOwnProperty(value);
  }

  // add(value) 往集合中添加 value
  add(value) {
    if (this.has(value)) return false;
    this.items[value] = value;
    return true;
  }

  // remove(value) 删除集合中指定的 value
  remove(value) {
    // 如果集合不存在该 value，返回 false
    if (!this.has(value)) return false;
    delete this.items[value];
  }

  // clear() 清空集合中所有 value
  clear() {
    this.items = {};
  }

  // size() 获取集合中的 value 个数
  size() {
    return Object.keys(this.items).length;
  }

  // values() 获取集合中所有的 value
  values() {
    return Object.keys(this.items);
  }

  // ------- 集合间的操作 ------- //
  // union() 求两个集合的并集
  union(otherSet) {
    // 1、创建一个新集合
    let unionSet = new Set();

    // 2、将当前集合（this）的所有 value，添加到新集合（unionSet）中
    for (let value of this.values()) {
      unionSet.add(value);
    }

    // 3、将 otherSet 集合的所有 value，添加到新集合（unionSet）中
    for (let value of otherSet.values()) {
      unionSet.add(value); // add() 已经有重复判断
    }

    return unionSet;
  }

  // intersection() 求两个集合的交集
  intersection(otherSet) {
    // 1、创建一个新集合
    let intersectionSet = new Set();

    // 2、从当前集合中取出每一个 value，判断是否在 otherSet 集合中存在
    for (let value of this.values()) {
      if (otherSet.has(value)) {
        intersectionSet.add(value);
      }
    }

    return intersectionSet;
  }

  // difference() 差集
  difference(otherSet) {
    // 1、创建一个新集合
    let differenceSet = new Set();

    // 2、从当前集合中取出每一个 value，判断是否在 otherSet 集合中存在，不存在的即为差集
    for (let value of this.values()) {
      if (!otherSet.has(value)) {
        differenceSet.add(value);
      }
    }

    return differenceSet;
  }

  // subset() 子集
  subset(otherSet) {
    // 从当前集合中取出每一个 value，判断是否在 otherSet 集合中存在，有不存在的返回 false
    // 遍历完所有的，返回 true
    for (let value of this.values()) {
      if (!otherSet.has(value)) {
        return false;
      }
    }
    return true;
  }
}

字典

字典

字典特点

  • 字典存储的是键值对，主要特点是一一对应。
  • 比如保存一个人的信息
    • 数组形式：[19，"Tom", 1.65]，可通过下标值取出信息。
    • 字典形式：{"age": 19, "name": "Tom", "height": 165}，可以通过 key 取出 value。
  • 此外，在字典中 key 是不能重复且无序的，而 Value 可以重复。

字典和映射的关系

  • 有些编程语言中称这种映射关系为字典，如 Swift 中的 Dictonary，Python 中的 dict。
  • 有些编程语言中称这种映射关系为 Map，比如 Java 中的 HashMap 和 TreeMap 等。

字典常见的操作

  • set(key,value) 向字典中添加新元素。
  • remove(key) 通过使用键值来从字典中移除键值对应的数据值。
  • has(key) 如果某个键值存在于这个字典中，则返回 true，反之则返回 false。
  • get(key) 通过键值查找特定的数值并返回。
  • clear() 将这个字典中的所有元素全部删除。
  • size() 返回字典所包含元素的数量。与数组的 length 属性类似。
  • keys() 将字典所包含的所有键名以数组形式返回。
  • values() 将字典所包含的所有数值以数组形式返回。

字典封装

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
// 字典结构的封装
export default class Map {
  constructor() {
    this.items = {};
  }

  // has(key) 判断字典中是否存在某个 key
  has(key) {
    return this.items.hasOwnProperty(key);
  }

  // set(key, value) 在字典中添加键值对
  set(key, value) {
    this.items[key] = value;
  }

  // remove(key) 在字典中删除指定的 key
  remove(key) {
    // 如果集合不存在该 key，返回 false
    if (!this.has(key)) return false;
    delete this.items[key];
  }

  // get(key) 获取指定 key 的 value，如果没有，返回 undefined
  get(key) {
    return this.has(key) ? this.items[key] : undefined;
  }

  // 获取所有的 key
  keys() {
    return Object.keys(this.items);
  }

  // 获取所有的 value
  values() {
    return Object.values(this.items);
  }

  // size() 获取字典中的键值对个数
  size() {
    return this.keys().length;
  }

  // clear() 清空字典中所有的键值对
  clear() {
    this.items = {};
  }
}

代码测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const map = new Map();

// set() 测试
map.set("name", "XPoet");
map.set("age", 18);
map.set("email", "i@xpoet.cn");
console.log(map); // {items: {name: "XPoet", age: 18, email: "i@xpoet.cn"}}

// has() 测试
console.log(map.has("name")); //--> true
console.log(map.has("address")); //--> false

// remove() 测试
map.remove("name");
console.log(map); // {age: 18, email: "i@xpoet.cn"}

// get() 测试
console.log(map.get("age")); //--> 18

// keys() 测试
console.log(map.keys()); //--> ["age", "email"]

// values() 测试
console.log(map.values()); //--> [18, "i@xpoet.cn"]

// size() 测试
console.log(map.size()); //--> 2

哈希表

认识哈希表

哈希表是一种非常重要的数据结构，几乎所有的编程语言都直接或者间接应用这种数据结构。

哈希表通常是基于数组实现的，但是相对于数组，它存在更多优势：

  • 哈希表可以提供非常快速的 插入-删除-查找 操作。
  • 无论多少数据，插入和删除值都只需接近常量的时间，即 O(1) 的时间复杂度。实际上，只需要几个机器指令即可完成。
  • 哈希表的速度比树还要快，基本可以瞬间查找到想要的元素。
  • 哈希表相对于树来说编码要简单得多。

哈希表同样存在不足之处：

  • 哈希表中的数据是没有顺序的，所以不能以一种固定的方式（比如从小到大 ）来遍历其中的元素。
  • 通常情况下，哈希表中的 key 是不允许重复的，不能放置相同的 key，用于保存不同的元素。

哈希表是什么？

  • 哈希表并不好理解，不像数组、链表和树等可通过图形的形式表示其结构和原理。
  • 哈希表的结构就是数组，但它神奇之处在于对下标值的一种变换，这种变换我们可以称之为哈希函数，通过哈希函数可以获取 HashCode。

通过以下案例了解哈希表：

  • 案例一：公司想要存储 1000 个人的信息，每一个工号对应一个员工的信息。若使用数组，增删数据时比较麻烦；使用链表，获取数据时比较麻烦。有没有一种数据结构，能把某一员工的姓名转换为它对应的工号，再根据工号查找该员工的完整信息呢？没错此时就可以使用哈希表的哈希函数来实现。

  • 案例二：存储联系人和对应的电话号码：当要查找张三（比如）的号码时，若使用数组：由于不知道存储张三数据对象的下标值，所以查找起来十分麻烦，使用链表时也同样麻烦。而使用哈希表就能通过哈希函数把张三这个名称转换为它对应的下标值，再通过下标值查找效率就非常高了。

也就是说：哈希表最后还是基于数据来实现的，只不过哈希表能够通过哈希函数把字符串转化为对应的下标值，建立字符串和下标值的映射关系。

认识哈希化

为了把字符串转化为对应的下标值，需要有一套编码系统，为了方便理解我们创建这样一套编码系统：比如 a 为 1，b 为 2，c 为 3，以此类推 z 为 26，空格为 27（不考虑大写情况）。

有了编码系统后，将字母转化为数字也有很多种方案：

  • 方案一：数字相加。

例如 cats 转化为数字：3 + 1 + 20 + 19 = 43，那么就把 43 作为 cats 单词的下标值储存在数组中；

但是这种方式会存在这样的问题：很多的单词按照该方式转化为数字后都是 43，比如 was。而在数组中一个下标值只能储存一个数据，所以该方式不合理。

  • 方案二：幂的连乘。

我们平时使用的大于 10 的数字，就是用幂的连乘来表示它的唯一性的。
比如： 6543 = 6 * 10^3 + 5 * 10^2 + 4 * 10 + 3；这样单词也可以用该种方式来表示：cats = 3 * 27^3 + 1 * 27^2 + 20 * 27 + 17 = 60337。

虽然该方式可以保证字符的唯一性，但是如果是较长的字符（如 aaaaaaaaaa）所表示的数字就非常大，此时要求很大容量的数组，然而其中却有许多下标值指向的是无效的数据（比如不存在 zxcvvv 这样的单词），造成了数组空间的浪费。

两种方案总结：

  • 第一种方案（让数字相加求和）产生的数组下标太少。
  • 第二种方案（与 27 的幂相乘求和）产生的数组下标又太多。

现在需要一种压缩方法，把幂的连乘方案系统中得到的巨大整数范围压缩到可接受的数组范围中。可以通过取余操作来实现。虽然取余操作得到的结构也有可能重复，但是可以通过其他方式解决。

哈希表的一些概念

  • 哈希化

    将大数字转化成数组范围内下标的过程，称之为哈希化。

  • 哈希函数

    我们通常会将单词转化成大数字，把大数字进行哈希化的代码实现放在一个函数中，该函数就称为哈希函数。

  • 哈希表

    对最终数据插入的数组进行整个结构的封装，得到的就是哈希表。

地址的冲突

在实际中，经过哈希函数哈希化过后得到的下标值可能有重复，这种情况称为冲突，冲突是不可避免的，我们只能解决冲突。

解决冲突常见的两种方案：链地址法（拉链法）和开放地址法。

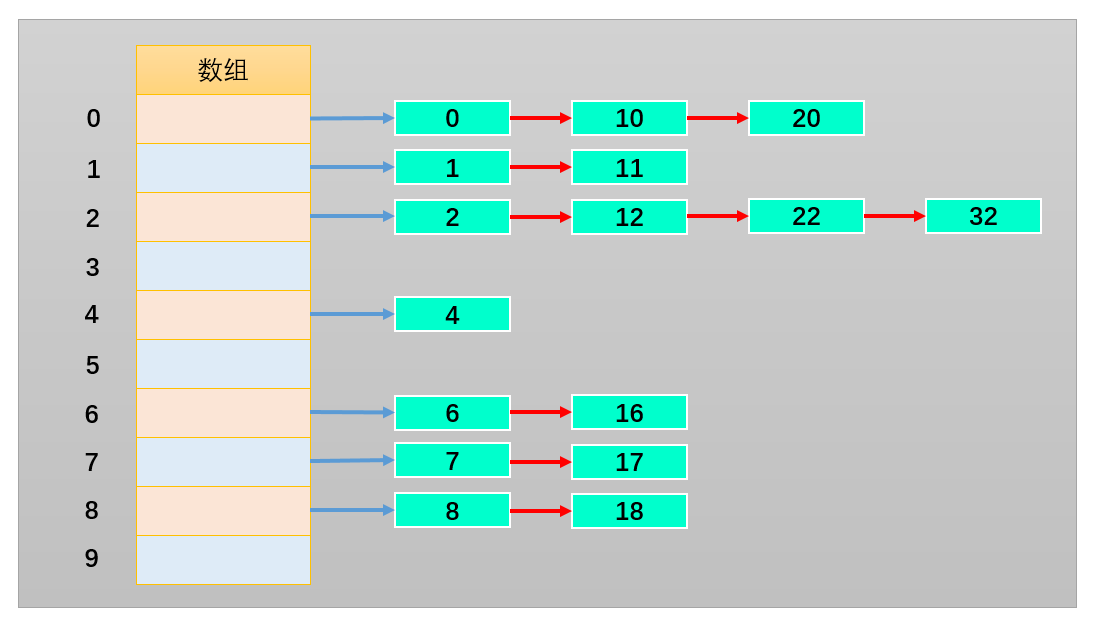
链地址法（拉链法）

如下图所示，我们将每一个数字都对 10 进行取余操作，则余数的范围 0~9 作为数组的下标值。并且，数组每一个下标值对应的位置存储的不再是一个数字了，而是存储由经过取余操作后得到相同余数的数字组成的数组或链表。

hZmGlV.png

这样可以根据下标值获取到整个数组或链表，之后继续在数组或链表中查找就可以了。而且，产生冲突的元素一般不会太多。

总结：链地址法解决冲突的办法是每个数组单元中存储的不再是单个数据，而是一条链条，这条链条常使用的数据结构为数组或链表，两种数据结构查找的效率相当（因为链条的元素一般不会太多）。

开放地址法

开放地址法的主要工作方式是寻找空白的单元格来放置冲突的数据项。

hZmrSx.png

根据探测空白单元格位置方式的不同，可分为三种方法：

  • 线性探测
  • 二次探测
  • 再哈希法
线性探测
  • 当插入 13 时：

经过哈希化（对 10 取余）之后得到的下标值 index=3，但是该位置已经放置了数据 33。而线性探测就是从 index 位置+1 开始向后一个一个来查找合适的位置来放置 13，所谓合适的位置指的是空的位置，如上图中 index=4 的位置就是合适的位置。

  • 当查询 13 时：

    • 首先 13 经过哈希化得到 index=3，如果 index=3 的位置存放的数据与需要查询的数据 13 相同，就直接返回；
      不相同时，则线性查找，从 index+1 位置开始一个一个位置地查找数据 13。
    • 查询过程中不会遍历整个哈希表，只要查询到空位置，就停止，因为插入 13 时不会跳过空位置去插入其他位置。

  • 当删除 13 时：

    • 删除操作和上述两种情况类似，但需要注意的是，删除一个数据项时，不能将该位置下标的内容设置为 null，否则会影响到之后其他的查询操作，因为一遇到为 null 的位置就会停止查找。
    • 通常删除一个位置的数据项时，我们可以将它进行特殊处理（比如设置为-1），这样在查找时遇到-1 就知道要继续查找。

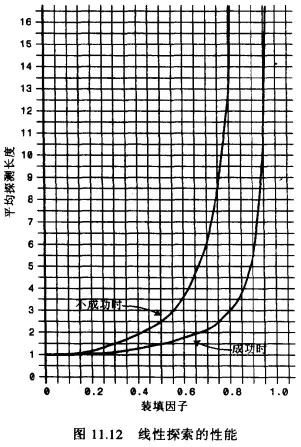
线性探测存在的问题：

  • 线性探测存在一个比较严重的问题，就是聚集。

  • 如哈希表中还没插入任何元素时，插入 23、24、25、26、27，这就意味着下标值为 3、4、5、6、7 的位置都放置了数据，这种一连串填充单元就称为聚集。

  • 聚集会影响哈希表的性能，无论是插入/查询/删除都会影响。

  • 比如插入 13 时就会发现，连续的单元 3~7 都不允许插入数据，并且在插入的过程中需要经历多次这种情况。二次探测法可以解决该问题。

hZm20e.png

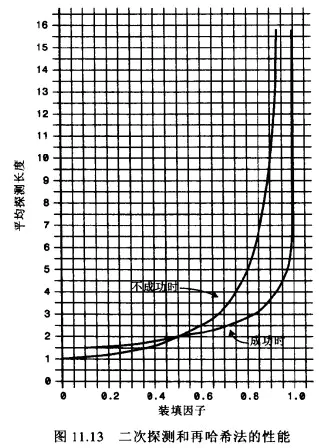
二次探测

上文所说的线性探测存在的问题：

  • 如果之前的数据是连续插入的，那么新插入的一个数据可能需要探测很长的距离；

    二次探测是在线性探测的基础上进行了优化：

  • 线性探测：我们可以看成是步长为 1 的探测，比如从下表值 x 开始，那么线性探测就是按照下标值：x+1、x+2、x+3 等依次探测；

  • 二次探测：对步长进行了优化，比如从下标值 x 开始探测：x+1^2^、x+2^2^、x+3^3^ 。这样一次性探测比较长的距离，避免了数据聚集带来的影响。

  • 二次探测存在的问题：

    当插入数据分布性较大的一组数据时，比如：13-163-63-3-213，这种情况会造成步长不一的一种聚集（虽然这种情况出现的概率较线性探测的聚集要小），同样会影响性能。

再哈希法

在开放地址法中寻找空白单元格的最好的解决方式为再哈希化。

  • 二次探测的步长是固定的：1，4，9，16 依次类推。
  • 现在需要一种方法：产生一种依赖关键字(数据)的探测序列，而不是每个关键字探测步长都一样。
  • 这样，不同的关键字即使映射到相同的数组下标，也可以使用不同的探测序列。
  • 再哈希法的做法为：把关键字用另一个哈希函数，再做一次哈希化，用这次哈希化的结果作为该关键字的步长。

第二次哈希化需要满足以下两点：

  • 和第一个哈希函数不同，不然哈希化后的结果仍是原来位置；
  • 不能输出为 0，否则每次探测都是原地踏步的死循环；

优秀的哈希函数：

  • stepSize = constant - （key % constant）；
  • 其中 constant 是质数，且小于数组的容量；
  • 例如：stepSize = 5 - （key % 5），满足需求，并且结果不可能为 0；

哈希化的效率

哈希表中执行插入和搜索操作效率是非常高的。

  • 如果没有发生冲突，那么效率就会更高；
  • 如果发生冲突，存取时间就依赖后来的探测长度；
  • 平均探测长度以及平均存取时间，取决于填装因子，随着填装因子变大，探测长度会越来越长。

装填因子

  • 装填因子表示当前哈希表中已经包含的数据项和整个哈希表长度的比值；
  • 装填因子 = 总数据项 / 哈希表长度；
  • 开放地址法的装填因子最大为 1，因为只有空白的单元才能放入元素；
  • 链地址法的装填因子可以大于 1，因为只要愿意，拉链法可以无限延伸下去；

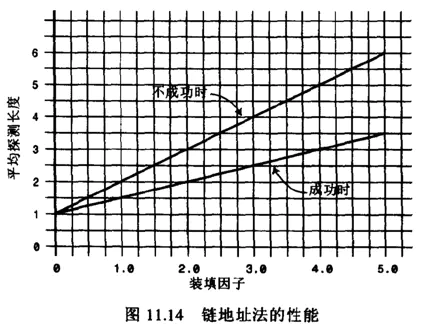
不同探测方式性能的比较

  • 线性探测

    可以看到，随着装填因子的增大，平均探测长度呈指数形式增长，性能较差。实际情况中，最好的装填因子取决于存储效率和速度之间的平衡，随着装填因子变小，存储效率下降，而速度上升。

    hZmo1P.png

  • 二次探测和再哈希化的性能

    二次探测和再哈希法性能相当，它们的性能比线性探测略好。由下图可知，随着装填因子的变大，平均探测长度呈指数形式增长，需要探测的次数也呈指数形式增长，性能不高。

    hZniBF.png

  • 链地址法的性能

    可以看到随着装填因子的增加，平均探测长度呈线性增长，较为平缓。在开发中使用链地址法较多，比如 Java 中的 HashMap 中使用的就是链地址法。

    hZnMnO.png

哈希函数

哈希表的优势在于它的速度，所以哈希函数不能采用消耗性能较高的复杂算法。提高速度的一个方法是在哈希函数中尽量减少乘法和除法。

性能高的哈希函数应具备以下两个优点：

  • 快速的计算；
  • 均匀的分布；

快速计算

霍纳法则：在中国霍纳法则也叫做秦久韶算法，具体算法为：

hZnrNj.png

求多项式的值时，首先计算最内层括号内一次多项式的值，然后由内向外逐层计算一次多项式的值。这种算法把求 n 次多项式 f(x)的值就转化为求 n 个一次多项式的值。

  • 变换之前：

    • 乘法次数：n(n+1)/2 次；
    • 加法次数：n 次；

  • 变换之后：

    • 乘法次数：n 次；
    • 加法次数：n 次；

如果使用大 O 表示时间复杂度的话，直接从变换前的 O(N^2)降到了 O(N)。

均匀分布

在设计哈希表时，我们已经有办法处理映射到相同下标值的情况：链地址法或者开放地址法。但是，为了提供效率，最好的情况还是让数据在哈希表中均匀分布。因此，我们需要在使用常量的地方，尽量使用质数。比如：哈希表的长度、N 次幂的底数等。

Java 中的 HashMap 采用的是链地址法，哈希化采用的是公式为：index = HashCode(key) & (Length-1) 即将数据化为二进制进行与运算，而不是取余运算。这样计算机直接运算二进制数据，效率更高。但是 JavaScript 在进行较大数据的与运算时会出现问题，所以我们使用 JavaScript 实现哈希化时采用取余运算。

封装哈希表

哈希表常见操作

  • put(key, value) 插入或修改操作。
  • get(key) 获取哈希表中特定位置的元素。
  • remove(key) 删除哈希表中特定位置的元素。
  • isEmpty() 如果哈希表中不包含任何元素，返回 trun，如果哈希表长度大于 0 则返回 false。
  • size() 返回哈希表包含的元素个数。
  • resize(value) 对哈希表进行扩容操作。

哈希函数的简单实现

首先使用霍纳法则计算 hashCode 的值，通过取余操作实现哈希化，此处先简单地指定数组的大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
hashFn(string, limit = 7) {

  // 自己采用的一个质数（无强制要求，质数即可）
  const PRIME = 31;

  // 1、定义存储 hashCode 的变量
  let hashCode = 0;

  // 2、使用霍纳法则（秦九韶算法），计算 hashCode 的值
  for (let item of string) {
    hashCode = PRIME * hashCode + item.charCodeAt();
  }

  // 3、对 hashCode 取余，并返回
  return hashCode % limit;
}

哈希函数测试

1
2
console.log(hashFn("123")); //--> 5
console.log(hashFn("abc")); //--> 6

哈希表的实现

创建哈希表类

封装的哈希表的数据结构模型：

hZnfDU.png

首先创建哈希表类 HashTable，并添加必要的属性和上面实现的哈希函数，再进行其他方法的实现。

1
2
3
4
5
6
7
class HashTable {
  constructor() {
    this.storage = []; // 哈希表存储数据的变量
    this.count = 0; // 当前存放的元素个数
    this.limit = 7; // 哈希表长度（初始设为质数 7）
  }
}

put(key,value)

哈希表的插入和修改操作是同一个函数：因为，当使用者传入一个 [key, value] 时，如果原来不存在该 key，那么就是插入操作，如果原来已经存在该 key，那么就是修改操作。

hZnjbD.png

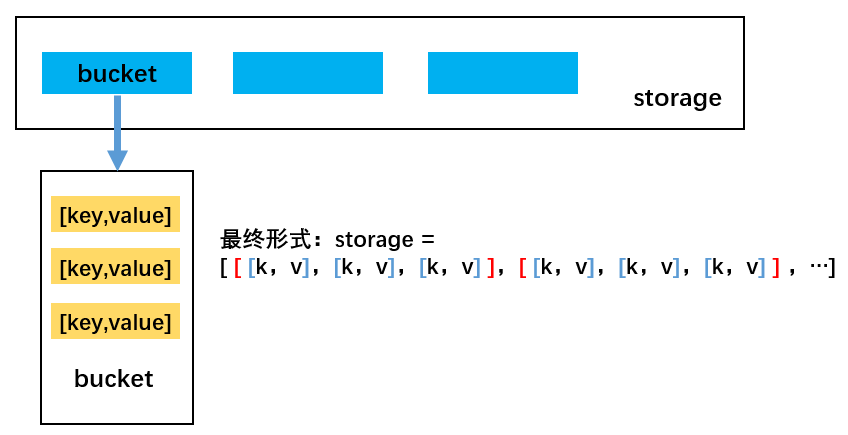
实现思路：

  • 首先，根据 key 获取索引值 index，目的为将数据插入到 storage 的对应位置；
  • 然后，根据索引值取出 bucket，如果 bucket 不存在，先创建 bucket，随后放置在该索引值的位置；
  • 接着，判断新增还是修改原来的值。如果已经有值了，就修改该值；如果没有，就执行后续操作。
  • 最后，进行新增数据操作。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// put(key, value) 往哈希表里添加数据
put(key, value) {

  // 1、根据 key 获取要映射到 storage 里面的 index（通过哈希函数获取）
  const index = hashFn(key, this.limit);

  // 2、根据 index 取出对应的 bucket
  let bucket = this.storage[index];

  // 3、判断是否存在 bucket
  if (bucket === undefined) {
    bucket = [];  // 不存在则创建
    this.storage[index] = bucket;
  }

  // 4、判断是插入数据操作还是修改数据操作
  for (let i = 0; i < bucket.length; i++) {
    let tuple = bucket[i]; // tuple 的格式：[key, value]
    if (tuple[0] === key) { // 如果 key 相等，则修改数据
      tuple[1] = value;
      return; // 修改完 tuple 里数据，return 终止不再往下执行。
    }
  }

  // 5、bucket 新增数据
  bucket.push([key, value]); // bucket 存储元组 tuple，格式为 [key, value]
  this.count++;

  // 判断哈希表是否要扩容，若装填因子 > 0.75，则扩容
  if (this.count / this.limit > this.loadFactor) {
    this.resize(this.getPrime(this.limit * 2));
  }

}

get(key)

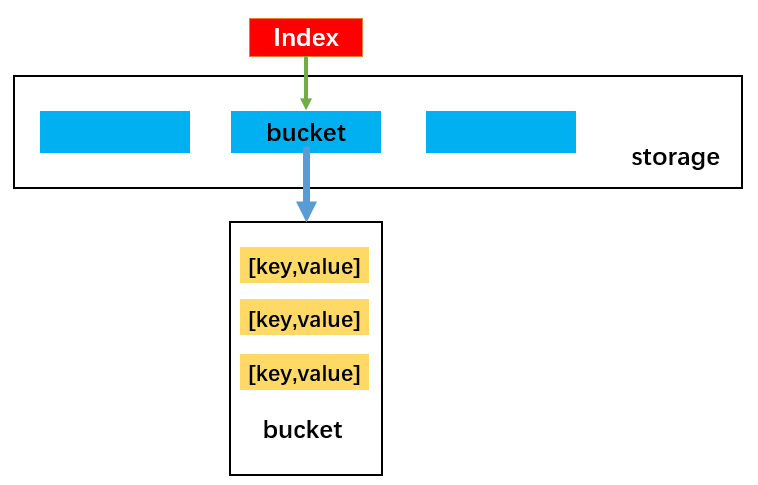
实现思路：

  • 首先，根据 key 通过哈希函数获取它在 storage 中对应的索引值 index。
  • 然后，根据索引值获取对应的 bucket。
  • 接着，判断获取到的 bucket 是否为 null，如果为 null，直接返回 null。
  • 随后，线性遍历 bucket 中每一个 key 是否等于传入的 key。如果等于，直接返回对应的 value。
  • 最后，遍历完 bucket 后，仍然没有找到对应的 key，直接 return null 即可。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 根据 get(key) 获取 value
get(key) {

  const index = hashFn(key, this.limit);
  const bucket = this.storage[index];

  if (bucket === undefined) {
    return null;
  }

  for (const tuple of bucket) {
    if (tuple[0] === key) {
      return tuple[1];
    }
  }
  return null;
}

remove(key)

实现思路：

  • 首先，根据 key 通过哈希函数获取它在 storage 中对应的索引值 index。
  • 然后，根据索引值获取对应的 bucket。
  • 接着，判断获取到的 bucket 是否为 null，如果为 null，直接返回 null。
  • 随后，线性查找 bucket，寻找对应的数据，并且删除。
  • 最后，依然没有找到，返回 null。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// remove(key) 删除指定 key 的数据
remove(key) {

  const index = hashFn(key, this.limit);
  const bucket = this.storage[index];

  if (bucket === undefined) {
    return null;
  }

  // 遍历 bucket，找到对应位置的 tuple，将其删除
  for (let i = 0, len = bucket.length; i < len; i++) {
    const tuple = bucket[i];
    if (tuple[0] === key) {
      bucket.splice(i, 1); // 删除对应位置的数组项
      this.count--;

      // 根据装填因子的大小，判断是否要进行哈希表压缩
      if (this.limit > 7 && this.count / this.limit < this.minLoadFactor) {
        this.resize(this.getPrime(Math.floor(this.limit / 2)));
      }

      return tuple;
    }

  }

}

isEmpty()

1
2
3
isEmpty() {
  return this.count === 0;
}

size()

1
2
3
size() {
  return this.count;
}

哈希表的扩容与压缩

为什么需要扩容？

  • 前面我们在哈希表中使用的是长度为 7 的数组，由于使用的是链地址法，装填因子(loadFactor)可以大于 1，所以这个哈希表可以无限制地插入新数据。

  • 但是，随着数据量的增多，storage 中每一个 index 对应的 bucket 数组（链表）就会越来越长，这就会造成哈希表效率的降低。

什么情况下需要扩容？

  • 常见的情况是 loadFactor > 0.75 的时候进行扩容。

如何进行扩容？

  • 简单的扩容可以直接扩大两倍（关于质数，之后讨论）。
  • 扩容之后所有的数据项都要进行同步修改。

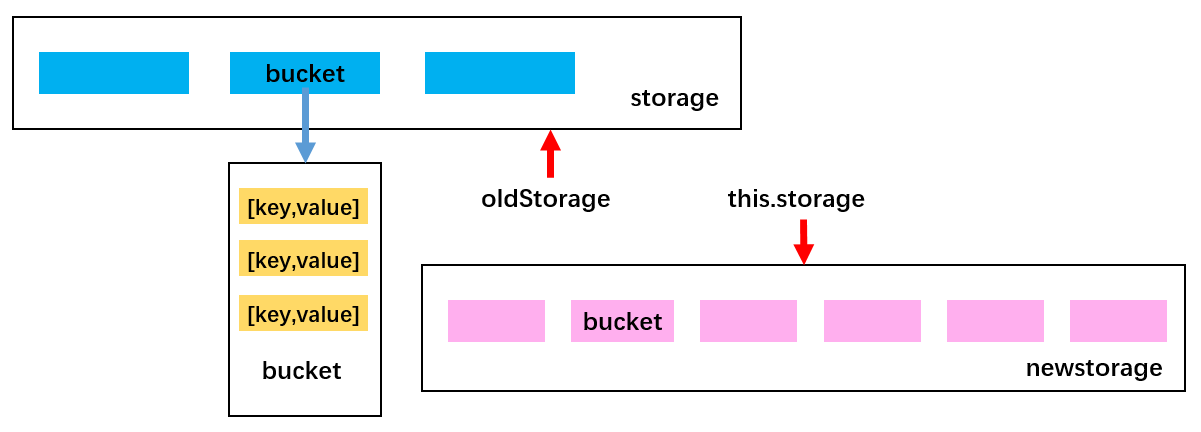
实现思路：

  • 首先，定义一个变量，比如 oldStorage 指向原来的 storage。
  • 然后，创建一个新的容量更大的数组，让 this.storage 指向它。
  • 最后，将 oldStorage 中的每一个 bucket 中的每一个数据取出来依次添加到 this.storage 指向的新数组中。

hZu6de.png

resize() 的实现

装填因子 = 哈希表中数据 / 哈希表长度，即 loadFactor = count / HashTable.length。

resize 方法，既可以实现哈希表的扩容，也可以实现哈希表容量的压缩。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 重新调整哈希表大小，扩容或压缩
resize(newLimit) {

  // 1、保存旧的 storage 数组内容
  const oldStorage = this.storage;

  // 2、重置所有属性
  this.storage = [];
  this.count = 0;
  this.limit = newLimit;

  // 3、遍历 oldStorage，取出所有数据，重新 put 到 this.storage
  for (const bucket of oldStorage) {
    if (bucket) {
      for (const b of bucket) {
        this.put(b[0], b[1]);
      }
    }

  }
}

  • 通常情况下当装填因子 laodFactor > 0.75 时，对哈希表进行扩容。在哈希表中的添加方法（push 方法）中添加如下代码，判断是否需要调用扩容函数进行扩容。

    1
    2
    3
    4
    // 判断哈希表是否要扩容，若装填因子 > 0.75，则扩容
    if (this.count / this.limit > this.loadFactor) {
      this.resize(this.getPrime(this.limit * 2));
    }

  • 当装填因子 laodFactor < 0.25 时，对哈希表容量进行压缩。在哈希表中的删除方法（remove 方法）中添加如下代码，判断是否需要调用扩容函数进行压缩。

    1
    2
    3
    4
    // 根据装填因子的大小，判断是否要进行哈希表压缩
    if (this.limit > 7 && this.count / this.limit < this.minLoadFactor) {
      this.resize(this.getPrime(Math.floor(this.limit / 2)));
    }

选择质数作为哈希表容量

质数判断

1 不是质数

  • 方法一：针对质数的特点：只能被 1 和 number 整除，不能被 2 ~ (number-1)整除。遍历 2 ~ (num-1) 。

    这种方法虽然能实现质数的判断，但是效率不高。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    function isPrime(number) {
      if (number <= 1) return false;
      for (let i = 2; i < number; i++) {
        if (number % i === 0) {
          return false;
        }
      }
      return true;
    }
    • 方法二：只需要遍历 2 ~ num 的平方根即可。该方法性能较好。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    function isPrime(number) {
      if (number <= 1 || number === 4) return false;
      const temp = Math.ceil(Math.sqrt(number));
      for (let i = 2; i < temp; i++) {
        if (number % i === 0) {
          return false;
        }
      }
      return true;
    }

实现扩容或压缩后的哈希表容量为质数

实现思路：

2 倍扩容或压缩之后，通过循环调用 isPrime 判断得到的容量是否为质数，不是则+1，直到是为止。比如原长度：7，2 倍扩容后长度为 14，14 不是质数，14 + 1 = 15 不是质数，15 + 1 = 16 不是质数，16 + 1 = 17 是质数，停止循环，由此得到质数 17。

  • 第一步：首先需要为 HashTable 类添加判断质数的 isPrime 方法和获取质数的 getPrime 方法：

    1
    2
    3
    4
    5
    6
    7
    // getPrime(number) 根据传入的 number 获取最临近的质数
    getPrime(number) {
      while (!isPrime(number)) {
        number++;
      }
      return number;
    }

  • 修改添加元素的 put 方法和删除元素的 remove 方法中关于数组扩容的相关操作：

    在 put 方法中添加如下代码：

    1
    2
    3
    4
    // 判断哈希表是否要扩容，若装填因子 > 0.75，则扩容
    if (this.count / this.limit > this.loadFactor) {
      this.resize(this.getPrime(this.limit * 2));
    }

    在 remove 方法中添加如下代码：

    1
    2
    3
    4
    // 根据装填因子的大小，判断是否要进行哈希表压缩
    if (this.limit > 7 && this.count / this.limit < this.minLoadFactor) {
      this.resize(this.getPrime(Math.floor(this.limit / 2)));
    }

哈希表完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
class HashTable {
  constructor() {
    this.storage = []; // 哈希表存储数据的变量
    this.count = 0; // 当前存放的元素个数
    this.limit = 7; // 哈希表长度（初始设为质数 7）

    // 装填因子(已有个数/总个数)
    this.loadFactor = 0.75;
    this.minLoadFactor = 0.25;
  }

  // getPrime(number) 根据传入的 number 获取最临近的质数
  getPrime(number) {
    while (!isPrime(number)) {
      number++;
    }
    return number;
  }

  // put(key, value) 往哈希表里添加数据
  put(key, value) {
    // 1、根据 key 获取要映射到 storage 里面的 index（通过哈希函数获取）
    const index = hashFn(key, this.limit);

    // 2、根据 index 取出对应的 bucket
    let bucket = this.storage[index];

    // 3、判断是否存在 bucket
    if (bucket === undefined) {
      bucket = []; // 不存在则创建
      this.storage[index] = bucket;
    }

    // 4、判断是插入数据操作还是修改数据操作
    for (let i = 0; i < bucket.length; i++) {
      let tuple = bucket[i]; // tuple 的格式：[key, value]
      if (tuple[0] === key) {
        // 如果 key 相等，则修改数据
        tuple[1] = value;
        return; // 修改完 tuple 里数据，return 终止，不再往下执行。
      }
    }

    // 5、bucket 新增数据
    bucket.push([key, value]); // bucket 存储元组 tuple，格式为 [key, value]
    this.count++;

    // 判断哈希表是否要扩容，若装填因子 > 0.75，则扩容
    if (this.count / this.limit > this.loadFactor) {
      this.resize(this.getPrime(this.limit * 2));
    }
  }

  // 根据 get(key) 获取 value
  get(key) {
    const index = hashFn(key, this.limit);
    const bucket = this.storage[index];

    if (bucket === undefined) {
      return null;
    }

    for (const tuple of bucket) {
      if (tuple[0] === key) {
        return tuple[1];
      }
    }
    return null;
  }

  // remove(key) 删除指定 key 的数据
  remove(key) {
    const index = hashFn(key, this.limit);
    const bucket = this.storage[index];

    if (bucket === undefined) {
      return null;
    }

    // 遍历 bucket，找到对应位置的 tuple，将其删除
    for (let i = 0, len = bucket.length; i < len; i++) {
      const tuple = bucket[i];
      if (tuple[0] === key) {
        bucket.splice(i, 1); // 删除对应位置的数组项
        this.count--;

        // 根据装填因子的大小，判断是否要进行哈希表压缩
        if (this.limit > 7 && this.count / this.limit < this.minLoadFactor) {
          this.resize(this.getPrime(Math.floor(this.limit / 2)));
        }

        return tuple;
      }
    }
  }

  isEmpty() {
    return this.count === 0;
  }

  size() {
    return this.count;
  }

  // 重新调整哈希表大小，扩容或压缩
  resize(newLimit) {
    // 1、保存旧的 storage 数组内容
    const oldStorage = this.storage;

    // 2、重置所有属性
    this.storage = [];
    this.count = 0;
    this.limit = newLimit;

    // 3、遍历 oldStorage，取出所有数据，重新 put 到 this.storage
    for (const bucket of oldStorage) {
      if (bucket) {
        for (const b of bucket) {
          this.put(b[0], b[1]);
        }
      }
    }
  }
}

树

树结构

什么是树？

真实的树：

hZKkWR.png

树的特点：

  • 树一般都有一个根，连接着根的是树干；
  • 树干会发生分叉，形成许多树枝，树枝会继续分化成更小的树枝；
  • 树枝的最后是叶子；

现实生活中很多结构都是树的抽象，模拟的树结构相当于旋转 180° 的树。

hZKQFH.png

树结构对比于数组/链表/哈希表有哪些优势呢？

数组：

  • 优点：可以通过下标值访问，效率高；
  • 缺点：查找数据时需要先对数据进行排序，生成有序数组，才能提高查找效率；并且在插入和删除元素时，需要大量的位移操作；

链表：

  • 优点：数据的插入和删除操作效率都很高；
  • 缺点：查找效率低，需要从头开始依次查找，直到找到目标数据为止；当需要在链表中间位置插入或删除数据时，插入或删除的效率都不高。

哈希表：

  • 优点：哈希表的插入/查询/删除效率都非常高；
  • 缺点：空间利用率不高，底层使用的数组中很多单元没有被利用；并且哈希表中的元素是无序的，不能按照固定顺序遍历哈希表中的元素；而且不能快速找出哈希表中最大值或最小值这些特殊值。

树结构：

  • 优点：树结构综合了上述三种结构的优点，同时也弥补了它们存在的缺点（虽然效率不一定都比它们高），比如树结构中数据都是有序的，查找效率高；空间利用率高；并且可以快速获取最大值和最小值等。

总的来说：每种数据结构都有自己特定的应用场景。

树结构：

  • 树（Tree）：由 n（n ≥ 0）个节点构成的有限集合。当 n = 0 时，称为空树。

  • 对于任意一棵非空树（n > 0），它具备以下性质：

    • 数中有一个称为根（Root）的特殊节点，用 r 表示；
    • 其余节点可分为 m（m > 0）个互不相交的有限集合 T1，T2，…，Tm，其中每个集合本身又是一棵树，称为原来树的子树（SubTree）。

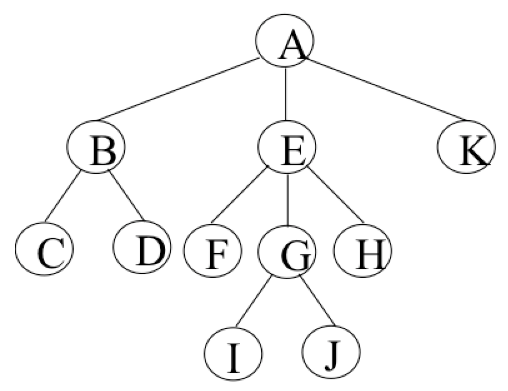
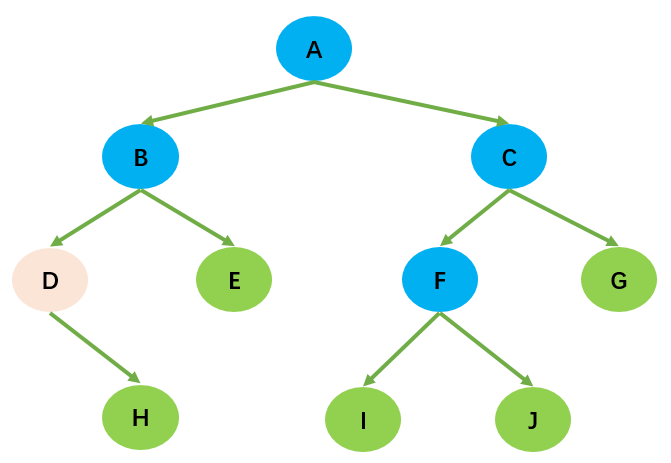
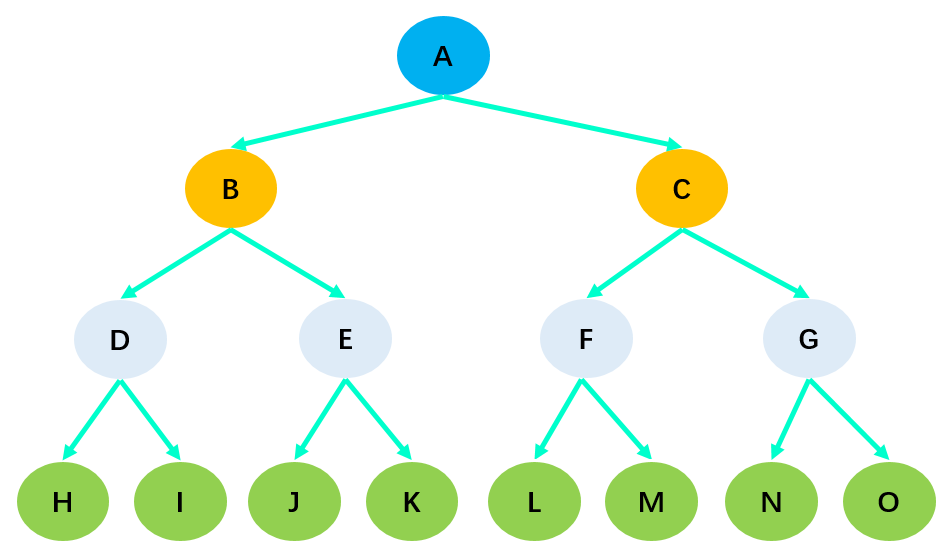
树的常用术语：

hZKNm8.png

  • 节点的度（Degree）：节点的子树个数，比如节点 B 的度为 2；
  • 树的度：树的所有节点中最大的度数，如上图树的度为 2；
  • 叶节点（Leaf）：度为 0 的节点（也称为叶子节点），如上图的 H，I 等；
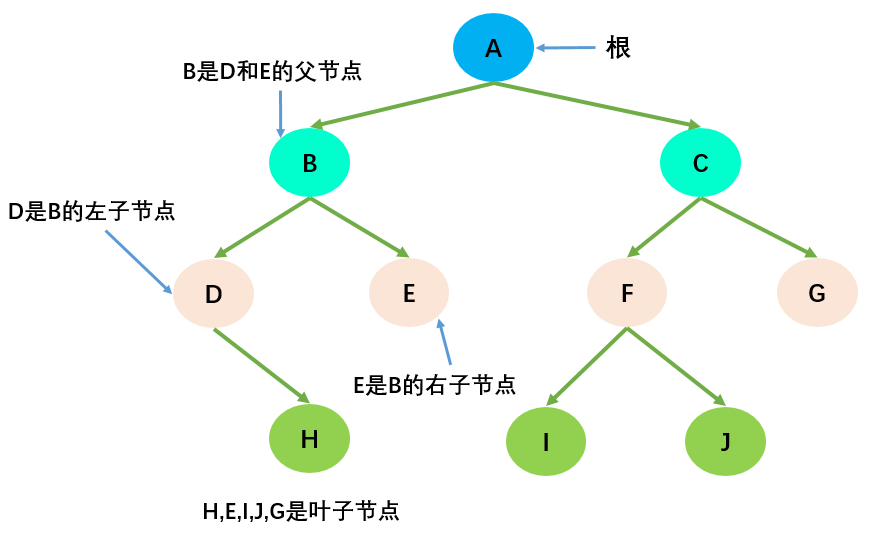
  • 父节点（Parent）：度不为 0 的节点称为父节点，如上图节点 B 是节点 D 和 E 的父节点；
  • 子节点（Child）：若 B 是 D 的父节点，那么 D 就是 B 的子节点；
  • 兄弟节点（Sibling）：具有同一父节点的各节点彼此是兄弟节点，比如上图的 B 和 C，D 和 E 互为兄弟节点；
  • 路径和路径长度：路径指的是一个节点到另一节点的通道，路径所包含边的个数称为路径长度，比如 A->H 的路径长度为 3；
  • 节点的层次（Level）：规定根节点在 1 层，其他任一节点的层数是其父节点的层数加 1。如 B 和 C 节点的层次为 2；
  • 树的深度（Depth）：树种所有节点中的最大层次是这棵树的深度，如上图树的深度为 4；

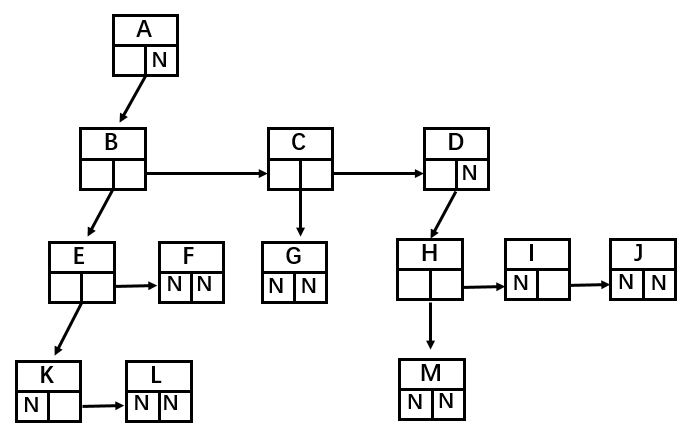
树结构的表示方式

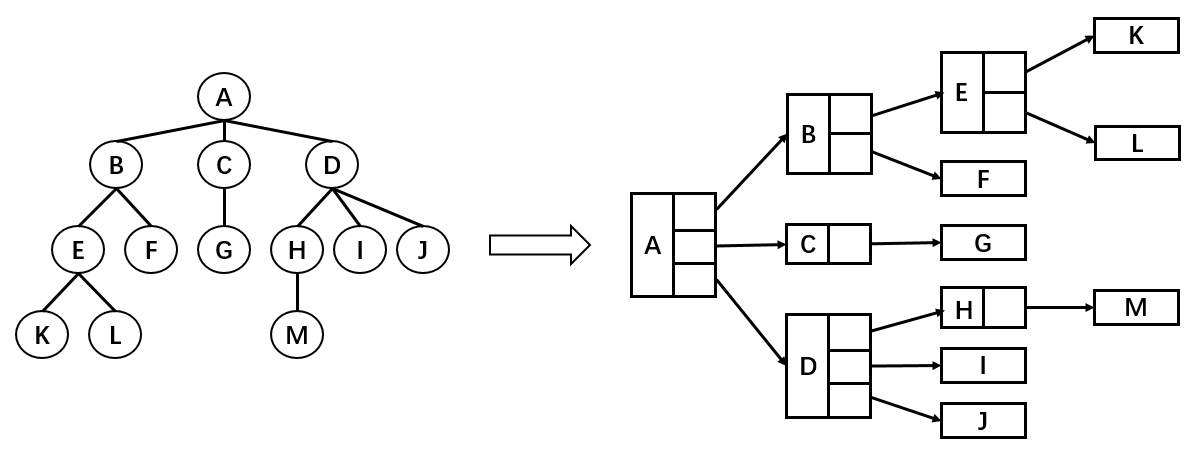
最普通的表示方法：

hZK20U.png

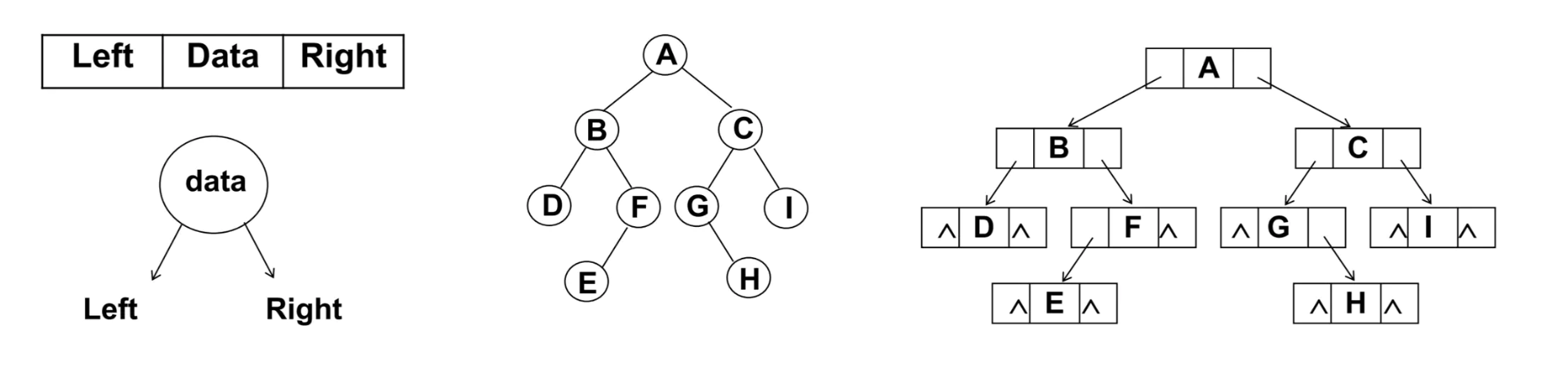
如图，树结构的组成方式类似于链表，都是由一个个节点连接构成。不过，根据每个父节点子节点数量的不同，每一个父节点需要的引用数量也不同。比如节点 A 需要 3 个引用，分别指向子节点 B，C，D；B 节点需要 2 个引用，分别指向子节点 E 和 F；K 节点由于没有子节点，所以不需要引用。

这种方法缺点在于我们无法确定某一结点的引用数。

儿子-兄弟表示法：

hZKbnK.png

这种表示方法可以完整地记录每个节点的数据，比如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//节点A
Node{
  //存储数据
  this.data = data
  //统一只记录左边的子节点
  this.leftChild = B
  //统一只记录右边的第一个兄弟节点
  this.rightSibling = null
}

//节点B
Node{
  this.data = data
  this.leftChild = E
  this.rightSibling = C
}

//节点F
Node{
  this.data = data
  this.leftChild = null
  this.rightSibling = null
}

这种表示法的优点在于每一个节点中引用的数量都是确定的。

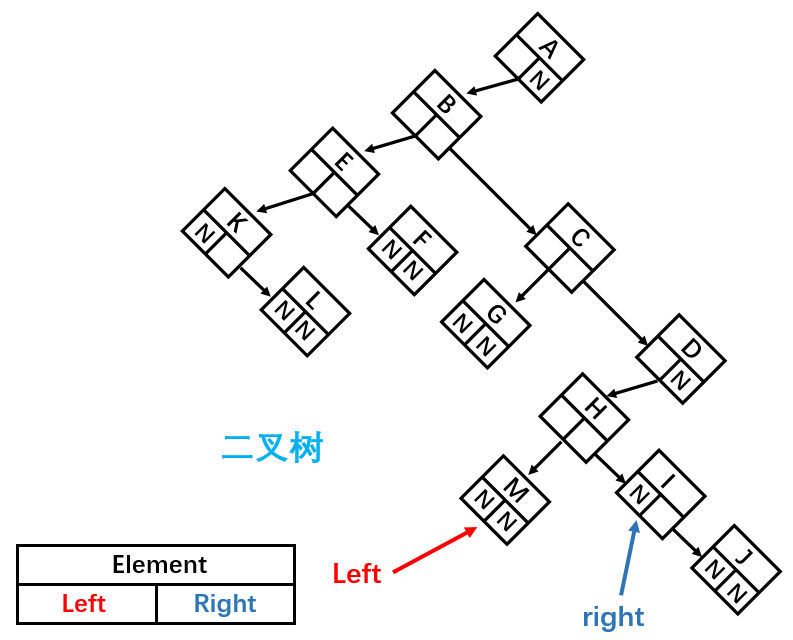
儿子-兄弟表示法旋转

以下为儿子-兄弟表示法组成的树结构：

hZMNg1.png

将其顺时针旋转 45° 之后：

hZM0HO.png

这样就成为了一棵二叉树，由此我们可以得出结论：任何树都可以通过二叉树进行模拟。但是这样父节点不是变了吗？其实，父节点的设置只是为了方便指向子节点，在代码实现中谁是父节点并没有关系，只要能正确找到对应节点即可。

二叉树

二叉树的概念

如果树中的每一个节点最多只能由两个子节点，这样的树就称为二叉树；

二叉树的组成

  • 二叉树可以为空，也就是没有节点；
  • 若二叉树不为空，则它由根节点和称为其左子树 TL 和右子树 TR 的两个不相交的二叉树组成；

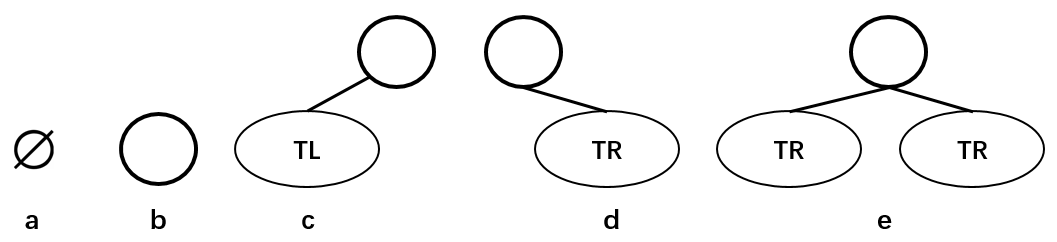
二叉树的五种形态

hZM7Cj.png

上图分别表示：空的二叉树、只有一个节点的二叉树、只有左子树 TL 的二叉树、只有右子树 TR 的二叉树和有左右两个子树的二叉树。

二叉树的特性

  • 一个二叉树的第 i 层的最大节点树为：2^(i-1)^，i >= 1；
  • 深度为 k 的二叉树的最大节点总数为：2^k^ - 1 ，k >= 1；
  • 对任何非空二叉树，若 n0 表示叶子节点的个数，n2表示度为 2 的非叶子节点个数，那么两者满足关系：n0 = n2 + 1；如下图所示：H，E，I，J，G 为叶子节点，总数为 5；A，B，C，F 为度为 2 的非叶子节点，总数为 4；满足 n0 = n2 + 1 的规律。

hZMXrV.png

特殊的二叉树

完美二叉树

完美二叉树（Perfect Binary Tree）也成为满二叉树（Full Binary Tree），在二叉树中，除了最下一层的叶子节点外，每层节点都有 2 个子节点，这就构成了完美二叉树。

hZQeaD.png

完全二叉树

完全二叉树（Complete Binary Tree）:

  • 除了二叉树最后一层外，其他各层的节点数都达到了最大值；
  • 并且，最后一层的叶子节点从左向右是连续存在，只缺失右侧若干叶子节点；
  • 完美二叉树是特殊的完全二叉树；

hZQzOP.png

在上图中，由于 H 缺失了右子节点，所以它不是完全二叉树。

二叉树的数据存储

常见的二叉树存储方式为数组和链表：

使用数组

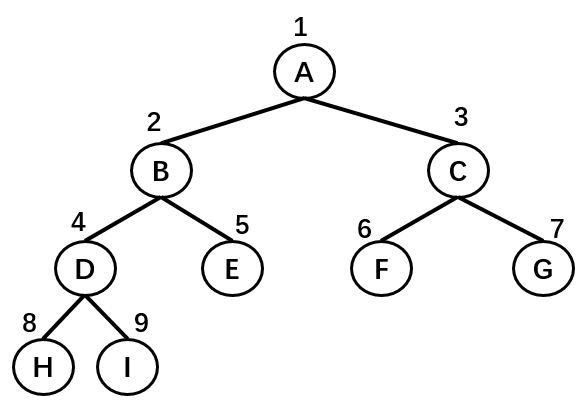
  • 完全二叉树：按从上到下，从左到右的方式存储数据。

hZlCTS.png

节点ABCDEFGHI
序号123456789

使用数组存储时，取数据的时候也十分方便：左子节点的序号等于父节点序号 _ 2，右子节点的序号等于父节点序号 _ 2 + 1 。

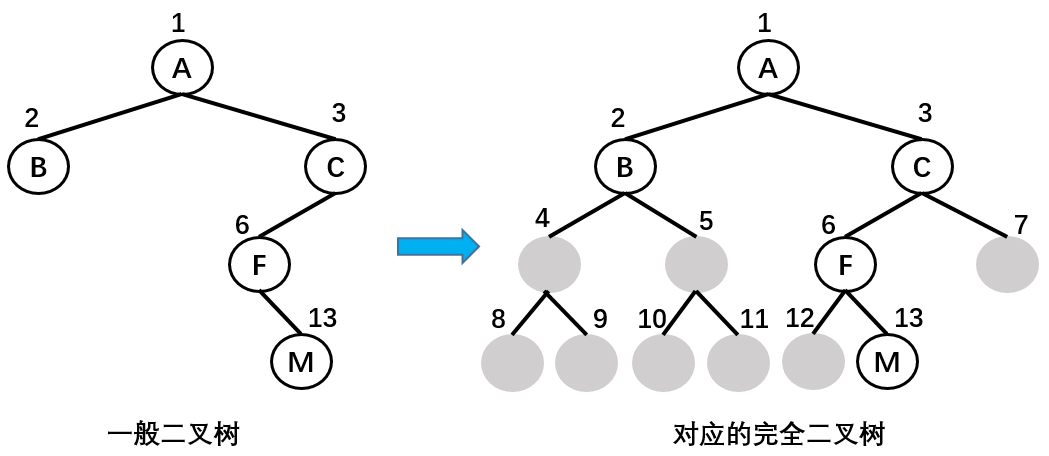
  • 非完全二叉树：非完全二叉树需要转换成完全二叉树才能按照上面的方案存储，这样会浪费很大的存储空间。

image

节点ABC^^F^^^^^^M
序号12345678910111213

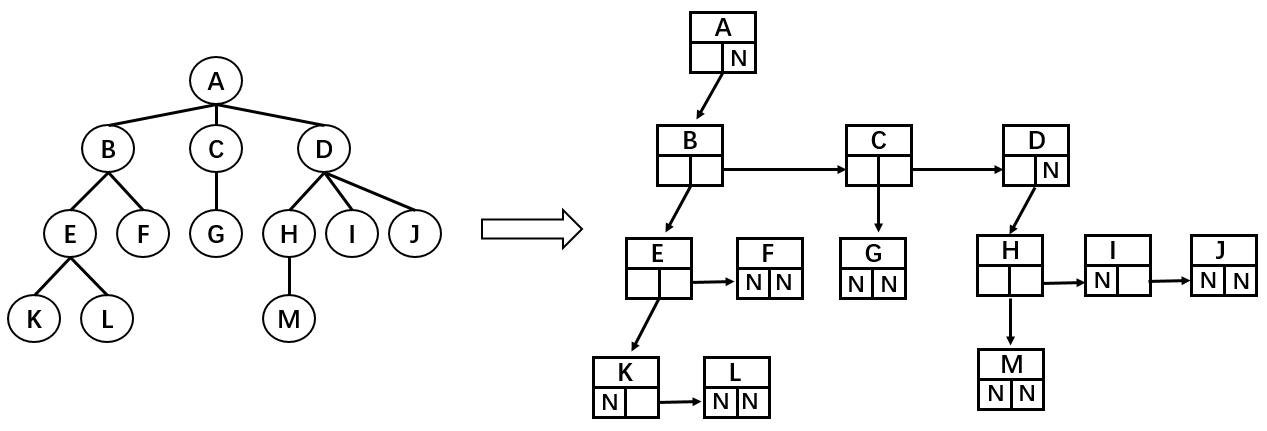
使用链表

二叉树最常见的存储方式为链表：每一个节点封装成一个 Node，Node 中包含存储的数据、左节点的引用和右节点的引用。

image

二叉搜索树

二叉搜索树

二叉搜索树（BST，Binary Search Tree），也称为二叉排序树和二叉查找树。

二叉搜索树是一棵二叉树，可以为空。

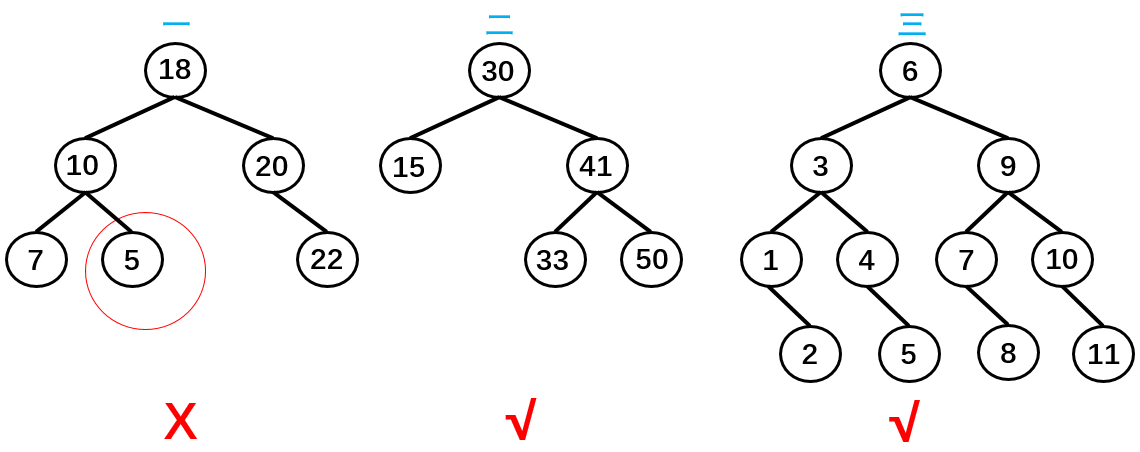
如果不为空，则满足以下性质：

  • 条件 1：非空左子树的所有键值小于其根节点的键值。比如三中节点 6 的所有非空左子树的键值都小于 6；
  • 条件 2：非空右子树的所有键值大于其根节点的键值；比如三中节点 6 的所有非空右子树的键值都大于 6；
  • 条件 3：左、右子树本身也都是二叉搜索树；

image

如上图所示，树二和树三符合 3 个条件属于二叉树，树一不满足条件 3 所以不是二叉树。

总结：二叉搜索树的特点主要是较小的值总是保存在左节点上，相对较大的值总是保存在右节点上。这种特点使得二叉搜索树的查询效率非常高，这也就是二叉搜索树中“搜索”的来源。

二叉搜索树应用举例

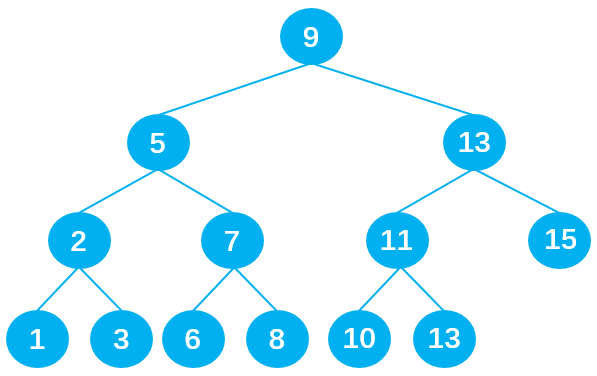
下面是一个二叉搜索树：

image

若想在其中查找数据 10，只需要查找 4 次，查找效率非常高。

  • 第 1 次：将 10 与根节点 9 进行比较，由于 10 > 9，所以 10 下一步与根节点 9 的右子节点 13 比较；
  • 第 2 次：由于 10 < 13，所以 10 下一步与父节点 13 的左子节点 11 比较；
  • 第 3 次：由于 10 < 11，所以 10 下一步与父节点 11 的左子节点 10 比较；
  • 第 4 次：由于 10 = 10，最终查找到数据 10 。

image

同样是 15 个数据，在排序好的数组中查询数据 10，需要查询 10 次：

image

其实：如果是排序好的数组，可以通过二分查找：第一次找 9，第二次找 13，第三次找 15…。我们发现如果把每次二分的数据拿出来以树的形式表示的话就是二叉搜索树。这就是数组二分法查找效率之所以高的原因。

二叉搜索树的封装

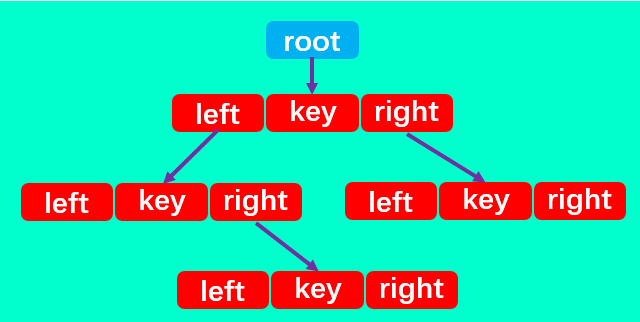
二叉搜索树有四个最基本的属性：指向节点的根（root），节点中的键（key）、左指针（right）、右指针（right）。

image

  • 所以，二叉搜索树中除了定义 root 属性外，还应定义一个节点内部类，里面包含每个节点中的 left、right 和 key 三个属性。

    1
    2
    3
    4
    5
    6
    7
    8
    // 节点类
    class Node {
      constructor(key) {
        this.key = key;
        this.left = null;
        this.right = null;
      }
    }

    二叉搜索树的常见操作：

    • insert(key) 向树中插入一个新的键。
    • search(key) 在树中查找一个键，如果节点存在，则返回 true；如果不存在，则返回 false。
    • preOrderTraverse 通过先序遍历方式遍历所有节点。
    • inOrderTraverse 通过中序遍历方式遍历所有节点。
    • postOrderTraverse 通过后序遍历方式遍历所有节点。
    • min 返回树中最小的值/键。
    • max 返回树中最大的值/键。
    • remove(key) 从树中移除某个键。

    插入数据

    实现思路：

    • 首先根据传入的 key 创建节点对象。
    • 然后判断根节点是否存在，不存在时通过：this.root = newNode，直接把新节点作为二叉搜索树的根节点。
    • 若存在根节点则重新定义一个内部方法 insertNode() 用于查找插入点。

    insert(key) 代码实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    // insert(key) 插入数据
    insert(key) {
      const newNode = new Node(key);

      if (this.root === null) {
        this.root = newNode;
      } else {
        this.insertNode(this.root, newNode);
      }

    }

    insertNode() 的实现思路:

    根据比较传入的两个节点，一直查找新节点适合插入的位置，直到成功插入新节点为止。

    • 当 newNode.key < node.key 向左查找:

      • 情况 1：当 node 无左子节点时，直接插入：

      • 情况 2：当 node 有左子节点时，递归调用 insertNode()，直到遇到无左子节点成功插入 newNode 后，不再符合该情况，也就不再调用 insertNode()，递归停止。

    • 当 newNode.key >= node.key 向右查找，与向左查找类似：

      • 情况 1：当 node 无右子节点时，直接插入：

      • 情况 2：当 node 有右子节点时，依然递归调用 insertNode()，直到遇到传入 insertNode 方法 的 node 无右子节点成功插入 newNode 为止。

    insertNode(root, node) 代码实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    insertNode(root, node) {

      if (node.key < root.key) { // 往左边查找插入

        if (root.left === null) {
          root.left = node;
        } else {
          this.insertNode(root.left, node);
        }

      } else { // 往右边查找插入

        if (root.right === null) {
          root.right = node;
        } else {
          this.insertNode(root.right, node);
        }

      }

    }

    遍历数据

    这里所说的树的遍历不仅仅针对二叉搜索树，而是适用于所有的二叉树。由于树结构不是线性结构，所以遍历方式有多种选择，常见的三种二叉树遍历方式为：

    • 先序遍历；
    • 中序遍历；
    • 后序遍历；

    还有层序遍历，使用较少。

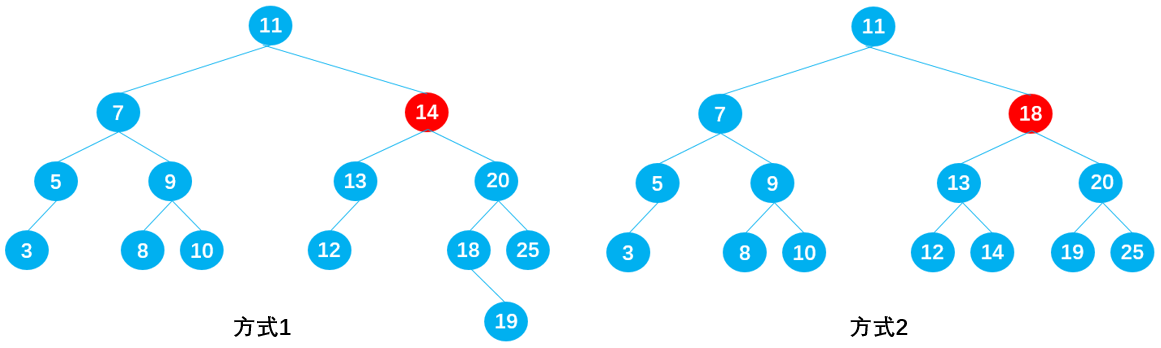
    先序遍历

    先序遍历的过程为：

    首先，遍历根节点；
    然后，遍历其左子树；
    最后，遍历其右子树；

    image

    如上图所示，二叉树的节点遍历顺序为：A -> B -> D -> H -> I -> E -> C -> F -> G。

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    // 先序遍历（根左右 DLR）
    preorderTraversal() {
      const result = [];
      this.preorderTraversalNode(this.root, result);
      return result;
    }

    preorderTraversalNode(node, result) {
      if (node === null) return result;
      result.push(node.key);
      this.preorderTraversalNode(node.left, result);
      this.preorderTraversalNode(node.right, result);
    }
    中序遍历

    实现思路：与先序遍历原理相同，只不过是遍历的顺序不一样了。

    首先，遍历其左子树；
    然后，遍历根（父）节点；
    最后，遍历其右子树；

    过程图解：

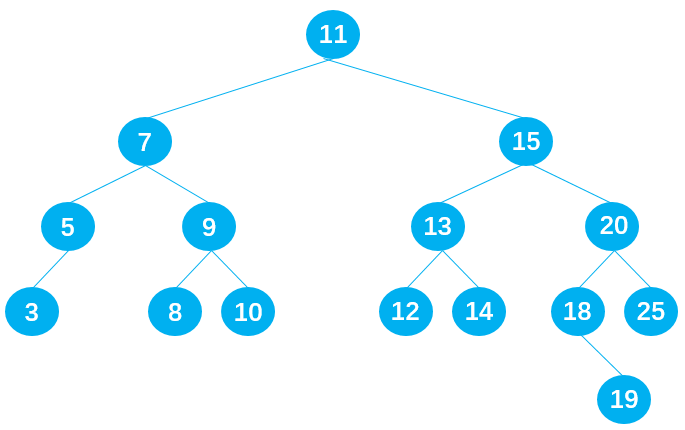
    image

    输出节点的顺序应为：3 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10 -> 11 -> 12 -> 13 -> 14 -> 15 -> 18 -> 20 -> 25 。

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    // 中序遍历（左根右 LDR）
    inorderTraversal() {
      const result = [];
      this.inorderTraversalNode(this.root, result);
      return result;
    }

    inorderTraversalNode(node, result) {
      if (node === null) return result;
      this.inorderTraversalNode(node.left, result);
      result.push(node.key);
      this.inorderTraversalNode(node.right, result);
    }
    后序遍历

    实现思路：与先序遍历原理相同，只不过是遍历的顺序不一样了。

    首先，遍历其左子树；
    然后，遍历其右子树；
    最后，遍历根（父）节点；

    过程图解：

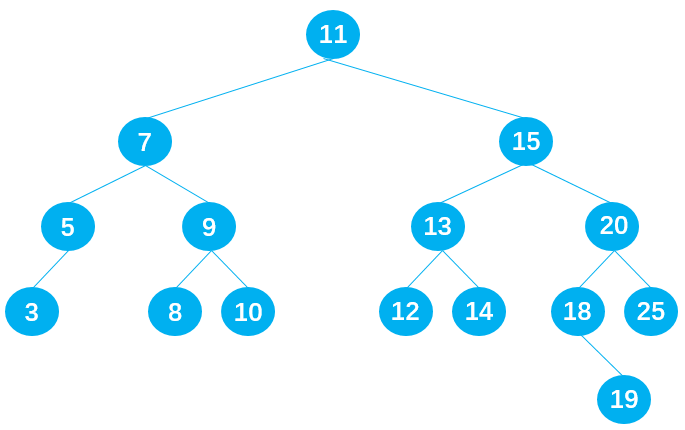
    image

    输出节点的顺序应为：3 -> 6 -> 5 -> 8 -> 10 -> 9 -> 7 -> 12 -> 14 -> 13 -> 18 -> 25 -> 20 -> 15 -> 11 。

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    // 后序遍历（左右根 LRD）
    postorderTraversal() {
      const result = [];
      this.postorderTraversalNode(this.root, result);
      return result;
    }

    postorderTraversalNode(node, result) {
      if (node === null) return result;
      this.postorderTraversalNode(node.left, result);
      this.postorderTraversalNode(node.right, result);
      result.push(node.key);
    }
    总结

    以遍历根（父）节点的顺序来区分三种遍历方式。比如：先序遍历先遍历根节点、中序遍历第二遍历根节点、后续遍历最后遍历根节点。

    查找数据

    查找最大值或最小值

    在二叉搜索树中查找最值非常简单，最小值在二叉搜索树的最左边，最大值在二叉搜索树的最右边。只需要一直向左/右查找就能得到最值，如下图所示：

    image

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    // min() 获取二叉搜索树最小值
    min() {
      if (!this.root) return null;
      let node = this.root;
      while (node.left !== null) {
        node = node.left;
      }
      return node.key;
    }

    // max() 获取二叉搜索树最大值
    max() {
      if (!this.root) return null;
      let node = this.root;
      while (node.right !== null) {
        node = node.right;
      }
      return node.key;
    }
    查找特定值

    查找二叉搜索树当中的特定值效率也非常高。只需要从根节点开始将需要查找节点的 key 值与之比较，若 node.key < root 则向左查找，若 node.key > root 就向右查找，直到找到或查找到 null 为止。这里可以使用递归实现，也可以采用循环来实现。

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    // search(key) 查找二叉搜索树中是否有相同的key，存在返回 true，否则返回 false
    search(key) {
      return this.searchNode(this.root, key);
    }

    // 通过递归实现
    searchNode(node, key) {
      if (node === null) return false;
      if (key < node.key) {
        return this.searchNode(node.left, key);
      } else if (key > node.key) {
        return this.searchNode(node.right, key);
      } else {
        return true;
      }
    }

    // 通过 while 循环实现
    search2(key) {

      let node = this.root;

      while (node !== null) {
        if (key < node.key) {
          node = node.left;
        } else if (key > node.key) {
          node = node.right;
        } else {
          return true;
        }
      }

      return false;

    }

    删除数据

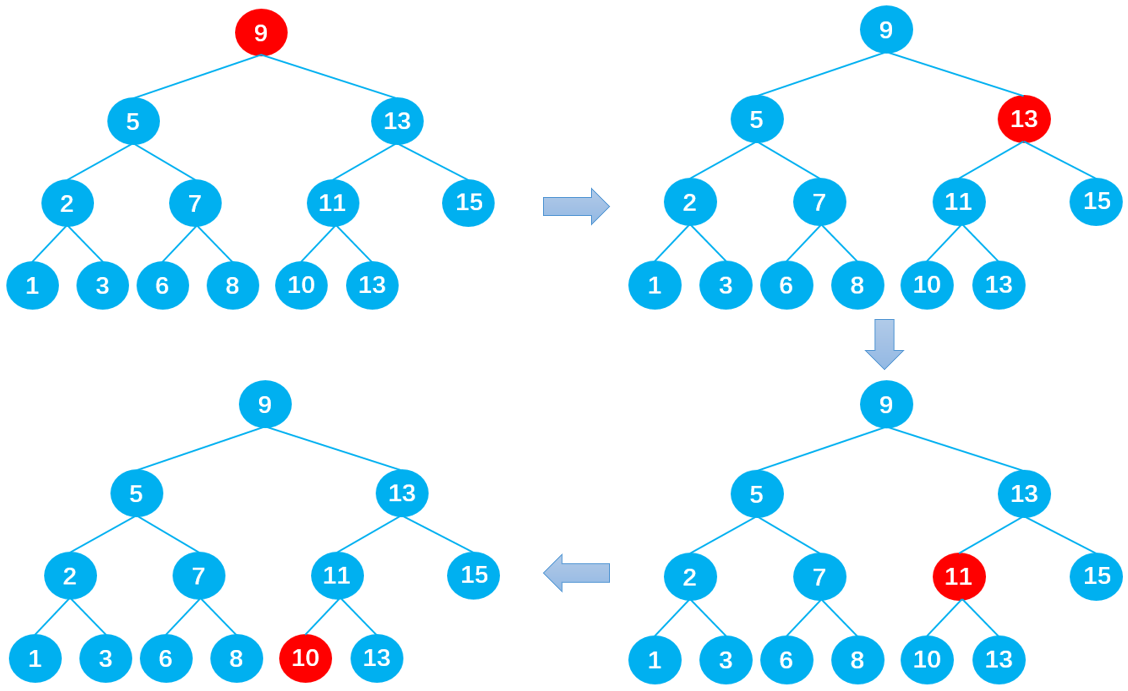
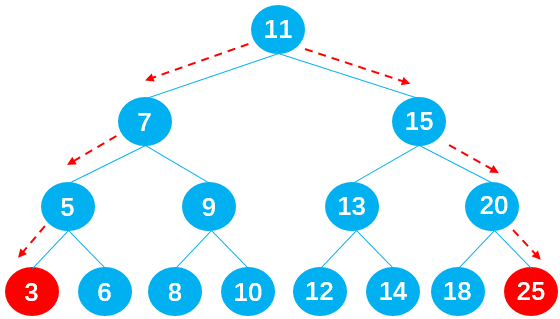
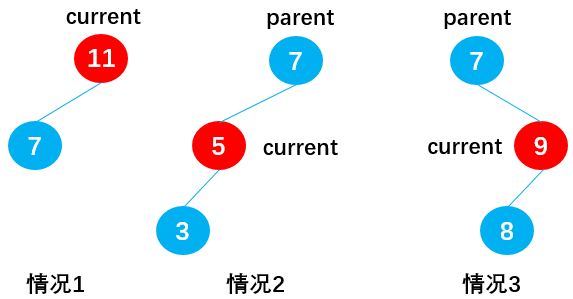
    实现思路：

    第一步：先找到需要删除的节点，若没找到，则不需要删除；

    首先定义变量 current 用于保存需要删除的节点、变量 parent 用于保存它的父节点、变量 isLeftChild 保存 current 是否为 parent 的左节点，这样方便之后删除节点时改变相关节点的指向。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    let currentNode = this.root;
    let parentNode = null;
    let isLeftChild = true;

    // 循环查找到要删除的节点 currentNode，以及它的 parentNode、isLeftChild
    while (currentNode.key !== key) {
      parentNode = currentNode;

      // 小于，往左查找
      if (key < currentNode.key) {
        isLeftChild = true;
        currentNode = currentNode.left;
      } else {
        // 否则往右查找
        isLeftChild = false;
        currentNode = currentNode.right;
      }

      // 找到最后都没找到相等的节点，返回 false
      if (currentNode === null) {
        return false;
      }
    }

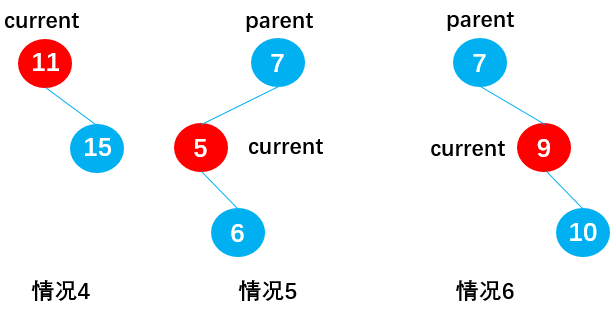
    第二步：删除找到的指定节点，后分 3 种情况：

    • 删除的是叶子节点；
    • 删除的是只有一个子节点的节点；
    • 删除的是有两个子节点的节点；
    删除的是叶子节点

    删除的是叶子节点分两种情况：

    • 叶子节点也是根节点

      当该叶子节点为根节点时，如下图所示，此时 current == this.root，直接通过：this.root = null，删除根节点。

      image

    • 叶子节点不为根节点

      当该叶子节点不为根节点时也有两种情况，如下图所示

      image

      若 current = 8，可以通过：parent.left = null，删除节点 8；

      若 current = 10，可以通过：parent.right = null，删除节点 10；

      代码实现：

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      // 1、删除的是叶子节点的情况
      if (currentNode.left === null && currentNode.right === null) {
        if (currentNode === this.root) {
          this.root = null;
        } else if (isLeftChild) {
          parentNode.left = null;
        } else {
          parentNode.right = null;
        }

        // 2、删除的是只有一个子节点的节点
      }
    删除的是只有一个子节点的节点

    有六种情况：

    当 current 存在左子节点时（current.right == null）：

    • 情况 1：current 为根节点（current == this.root），如节点 11，此时通过：this.root = current.left，删除根节点 11；

    • 情况 2：current 为父节点 parent 的左子节点（isLeftChild == true），如节点 5，此时通过：parent.left = current.left，删除节点 5；

    • 情况 3：current 为父节点 parent 的右子节点（isLeftChild == false），如节点 9，此时通过：parent.right = current.left，删除节点 9；

    image

    当 current 存在右子节点时（current.left = null）：

    • 情况 4：current 为根节点（current == this.root），如节点 11，此时通过：this.root = current.right，删除根节点 11。

    • 情况 5：current 为父节点 parent 的左子节点（isLeftChild == true），如节点 5，此时通过：parent.left = current.right，删除节点 5；

    • 情况 6：current 为父节点 parent 的右子节点（isLeftChild == false），如节点 9，此时通过：parent.right = current.right，删除节点 9；

    image

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    // 2、删除的是只有一个子节点的节点
    } else if (currentNode.right === null) { // currentNode 只存在左节点
      //-- 2.1、currentNode 只存在<左节点>的情况
      //---- 2.1.1、currentNode 等于 root
      //---- 2.1.2、parentNode.left 等于 currentNode
      //---- 2.1.3、parentNode.right 等于 currentNode

      if (currentNode === this.root) {
        this.root = currentNode.left;
      } else if (isLeftChild) {
        parentNode.left = currentNode.left;
      } else {
        parentNode.right = currentNode.left;
      }

    } else if (currentNode.left === null) { // currentNode 只存在右节点
      //-- 2.2、currentNode 只存在<右节点>的情况
      //---- 2.1.1 currentNode 等于 root
      //---- 2.1.1 parentNode.left 等于 currentNode
      //---- 2.1.1 parentNode.right 等于 currentNode

      if (currentNode === this.root) {
        this.root = currentNode.right;
      } else if (isLeftChild) {
        parentNode.left = currentNode.right;
      } else {
        parentNode.right = currentNode.right;
      }
    删除的是有两个子节点的节点

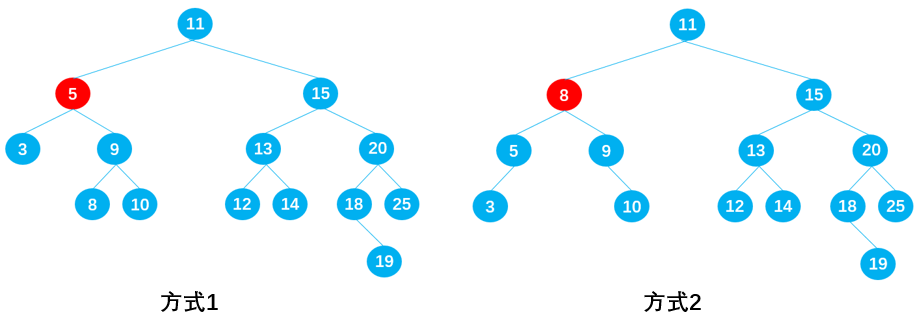
    这种情况十分复杂，首先依据以下二叉搜索树，讨论这样的问题：

    image

    删除节点 9

    在保证删除节点 9 后原二叉树仍为二叉搜索树的前提下，有两种方式：

    • 方式 1：从节点 9 的左子树中选择一合适的节点替代节点 9，可知节点 8 符合要求；
    • 方式 2：从节点 9 的右子树中选择一合适的节点替代节点 9，可知节点 10 符合要求；

    image

    删除节点 7

    在保证删除节点 7 后原二叉树仍为二叉搜索树的前提下，也有两种方式：

    • 方式 1：从节点 7 的左子树中选择一合适的节点替代节点 7，可知节点 5 符合要求；
    • 方式 2：从节点 7 的右子树中选择一合适的节点替代节点 7，可知节点 8 符合要求；

    image

    删除节点 15

    在保证删除节点 15 后原树二叉树仍为二叉搜索树的前提下，同样有两种方式：

    • 方式 1：从节点 15 的左子树中选择一合适的节点替代节点 15，可知节点 14 符合要求；
    • 方式 2：从节点 15 的右子树中选择一合适的节点替代节点 15，可知节点 18 符合要求；

    image

    相信你已经发现其中的规律了！

    规律总结：如果要删除的节点有两个子节点，甚至子节点还有子节点，这种情况下需要从要删除节点下面的子节点中找到一个合适的节点，来替换当前的节点。

    若用 current 表示需要删除的节点，则合适的节点指的是：

    • current 左子树中比 current 小一点点的节点，即 current 左子树中的最大值；
    • current 右子树中比 current 大一点点的节点，即 current 右子树中的最小值；
    前驱&后继

    在二叉搜索树中，这两个特殊的节点有特殊的名字：

    • 比 current 小一点点的节点，称为 current 节点的前驱。比如下图中的节点 5 就是节点 7 的前驱；
    • 比 current 大一点点的节点，称为 current 节点的后继。比如下图中的节点 8 就是节点 7 的后继；

    image

    查找需要被删除的节点 current 的后继时，需要在 current 的右子树中查找最小值，即在 current 的右子树中一直向左遍历查找；

    查找前驱时，则需要在 current 的左子树中查找最大值，即在 current 的左子树中一直向右遍历查找。

    下面只讨论查找 current 后继的情况，查找前驱的原理相同，这里暂不讨论。

    代码实现：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
      // 3、删除的是有两个子节点的节点
      } else {

        // 1、找到后续节点
        let successor = this.getSuccessor(currentNode);

        // 2、判断是否为根节点
        if (currentNode === this.root) {
          this.root = successor;
        } else if (isLeftChild) {
          parentNode.left = successor;
        } else {
          parentNode.right = successor;
        }

        // 3、将后续的左节点改为被删除的左节点
        successor.left = currentNode.left;
      }
    }

    // 获取后续节点，即从要删除的节点的右边开始查找最小的值
    getSuccessor(delNode) {

      // 定义变量，保存要找到的后续
      let successor = delNode;
      let current = delNode.right;
      let successorParent = delNode;

      // 循环查找 current 的右子树节点
      while (current !== null) {
        successorParent = successor;
        successor = current;
        current = current.left;
      }

      // 判断寻找到的后续节点是否直接就是要删除节点的 right
      if (successor !== delNode.right) {
        successorParent.left = successor.right;
        successor.right = delNode.right;
      }
      return successor;
    }
    完整实现
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    113
    114
    // 删除节点
    remove(key) {

      let currentNode = this.root;
      let parentNode = null;
      let isLeftChild = true;

      // 循环查找到要删除的节点 currentNode，以及它的 parentNode、isLeftChild
      while (currentNode.key !== key) {

        parentNode = currentNode;

        // 小于，往左查找
        if (key < currentNode.key) {
          isLeftChild = true;
          currentNode = currentNode.left;

        } else {  // 否则往右查找
          isLeftChild = false;
          currentNode = currentNode.right;
        }

        // 找到最后都没找到相等的节点，返回 false
        if (currentNode === null) {
          return false;
        }

      }


      // 1、删除的是叶子节点的情况
      if (currentNode.left === null && currentNode.right === null) {

        if (currentNode === this.root) {
          this.root = null;
        } else if (isLeftChild) {
          parentNode.left = null;
        } else {
          parentNode.right = null;
        }


        // 2、删除的是只有一个子节点的节点
      } else if (currentNode.right === null) { // currentNode 只存在左节点
        //-- 2.1、currentNode 只存在<左节点>的情况
        //---- 2.1.1、currentNode 等于 root
        //---- 2.1.2、parentNode.left 等于 currentNode
        //---- 2.1.3、parentNode.right 等于 currentNode

        if (currentNode === this.root) {
          this.root = currentNode.left;
        } else if (isLeftChild) {
          parentNode.left = currentNode.left;
        } else {
          parentNode.right = currentNode.left;
        }

      } else if (currentNode.left === null) { // currentNode 只存在右节点
        //-- 2.2、currentNode 只存在<右节点>的情况
        //---- 2.1.1 currentNode 等于 root
        //---- 2.1.1 parentNode.left 等于 currentNode
        //---- 2.1.1 parentNode.right 等于 currentNode

        if (currentNode === this.root) {
          this.root = currentNode.right;
        } else if (isLeftChild) {
          parentNode.left = currentNode.right;
        } else {
          parentNode.right = currentNode.right;
        }


        // 3、删除的是有两个子节点的节点
      } else {

        // 1、找到后续节点
        let successor = this.getSuccessor(currentNode);

        // 2、判断是否为根节点
        if (currentNode === this.root) {
          this.root = successor;
        } else if (isLeftChild) {
          parentNode.left = successor;
        } else {
          parentNode.right = successor;
        }

        // 3、将后续的左节点改为被删除的左节点
        successor.left = currentNode.left;
      }
    }

    // 获取后续节点，即从要删除的节点的右边开始查找最小的值
    getSuccessor(delNode) {

      // 定义变量，保存要找到的后续
      let successor = delNode;
      let current = delNode.right;
      let successorParent = delNode;

      // 循环查找 current 的右子树节点
      while (current !== null) {
        successorParent = successor;
        successor = current;
        current = current.left;
      }

      // 判断寻找到的后续节点是否直接就是要删除节点的 right
      if (successor !== delNode.right) {
        successorParent.left = successor.right;
        successor.right = delNode.right;
      }
      return successor;
    }

    平衡树

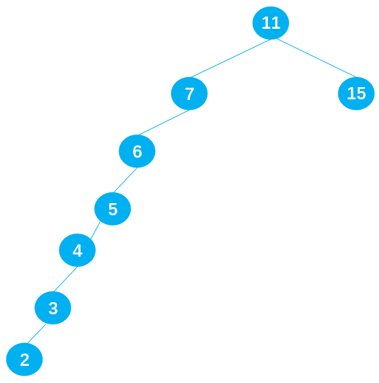
    二叉搜索树的缺陷：当插入的数据是有序的数据，就会造成二叉搜索树的深度过大。比如原二叉搜索树由 11 7 15 组成，如下图所示：

    image

    当插入一组有序数据：6 5 4 3 2 就会变成深度过大的搜索二叉树，会严重影响二叉搜索树的性能。

    image

    非平衡树

    • 比较好的二叉搜索树，它的数据应该是左右均匀分布的。
    • 但是插入连续数据后，二叉搜索树中的数据分布就变得不均匀了，我们称这种树为非平衡树。
    • 对于一棵平衡二叉树来说，插入/查找等操作的效率是 O(log n)。
    • 而对于一棵非平衡二叉树来说，相当于编写了一个链表，查找效率变成了 O(n)。

    树的平衡性

    为了能以较快的时间 O(log n)来操作一棵树，我们需要保证树总是平衡的：

    • 起码大部分是平衡的，此时的时间复杂度也是接近 O(log n) 的；
    • 这就要求树中每个节点左边的子孙节点的个数，应该尽可能地等于右边的子孙节点的个数；

    常见的平衡树

    • AVL 树：是最早的一种平衡树，它通过在每个节点多存储一个额外的数据来保持树的平衡。由于 AVL 树是平衡树，所以它的时间复杂度也是 O(log n)。但是它的整体效率不如红黑树，开发中比较少用。
    • 红黑树：同样通过一些特性来保持树的平衡，时间复杂度也是 O(log n)。进行插入/删除等操作时，性能优于 AVL 树，所以平衡树的应用基本都是红黑树。

图

图的概念

在计算机程序设计中，图也是一种非常常见的数据结构，图论其实是一个非常大的话题，在数学上起源于哥尼斯堡七桥问题。

什么是图？

  • 图是一种与树有些相似的数据结构。

    • 实际上，在数学的概念上，树是图的一种。
    • 我们知道树可以用来模拟很多现实的数据结构，比如：家谱/公司组织架构等等。

  • 那么图长什么样子呢？或者什么样的数据使用图来模拟更合适呢？

    • 人与人之间的关系网
      image

    • 互联网中的网络关系
      image

    • 广州地铁图
      image

  • 那么，什么是图呢?

    • 我们会发现，上面的结点（其实图中叫顶点 Vertex）之间的关系，是不能使用树来表示（几叉树都不可以）。
    • 这个时候，我们就可以使用图来模拟它们。

  • 图通常有什么特点呢？

    • 一组顶点：通常用 V (Vertex) 表示顶点的集合
    • 一组边：通常用 E (Edge) 表示边的集合
    • 边是顶点和顶点之间的连线
    • 边可以是有向的，也可以是无向的。（比如 A — B，通常表示无向。 A –> B，通常表示有向）

图的术语

术语

  • 我们在学习树的时候，树有很多的其他术语，了解这些术语有助于我们更深层次的理解图。

  • 但是图的术语其实非常多，如果你找一本专门讲图的各个方面的书籍，会发现只是术语就可以占据一个章节。

  • 这里，这里介绍几个比较常见的术语，某些术语后面用到的时候，再了解，没有用到的，不做赘述。

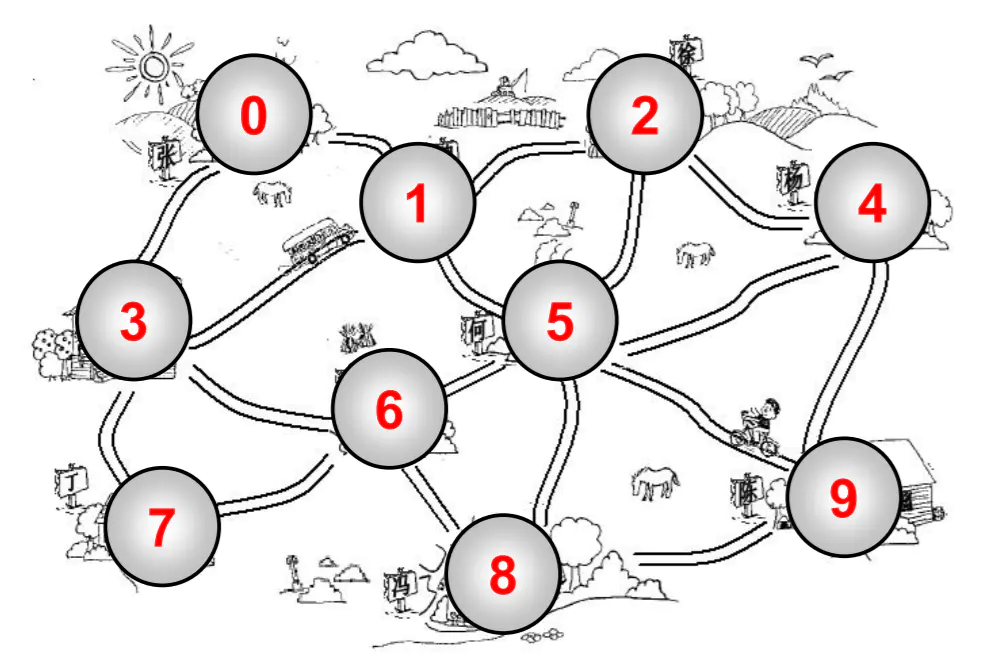
  • 下面这是个抽象出来的图
    image

  • 顶点

    • 顶点刚才我们已经介绍过了，表示图中的一个结点。
    • 比如地铁站中某个站/多个村庄中的某个村庄/互联网中的某台主机/人际关系中的人。

  • 边

    • 边表示顶点和顶点之间的连线。
    • 比如地铁站中两个站点之间的直接连线, 就是一个边。
    • 注意：这里的边不要叫做路径，路径有其他的概念，后面会区分。

  • 相邻顶点

    • 由一条边连接在一起的顶点称为相邻顶点。
    • 比如 0 - 1 是相邻的，0 - 3 是相邻的。0 - 2 是不相邻的。

  • 度

    • 一个顶点的度是相邻顶点的数量
    • 比如 0 顶点和其他两个顶点相连，0 顶点的度是 2
    • 比如 1 顶点和其他四个顶点相连，1 顶点的度是 4

  • 路径

    • 路径是顶点 v1，v2…，vn 的一个连续序列, 比如上图中 0 1 5 9 就是一条路径。
    • 简单路径: 简单路径要求不包含重复的顶点. 比如 0 1 5 9 是一条简单路径。
    • 回路：第一个顶点和最后一个顶点相同的路径称为回路。比如 0 1 5 6 3 0。

  • 无向图

    • 上面的图就是一张无向图，因为所有的边都没有方向。
    • 比如 0 - 1 之间有变，那么说明这条边可以保证 0 -> 1，也可以保证 1 -> 0。

  • 有向图

    • 有向图表示的图中的边是有方向的。
    • 比如 0 -> 1，不能保证一定可以 1 -> 0，要根据方向来定。

无权图和带权图

  • 无权图

    • 我们上面的图就是一张无权图（边没有携带权重）
    • 我们上面的图中的边是没有任何意义的，不能收 0 - 1 的边，比 4 - 9 的边更远或者用的时间更长。

  • 带权图

    • 带权图表示边有一定的权重
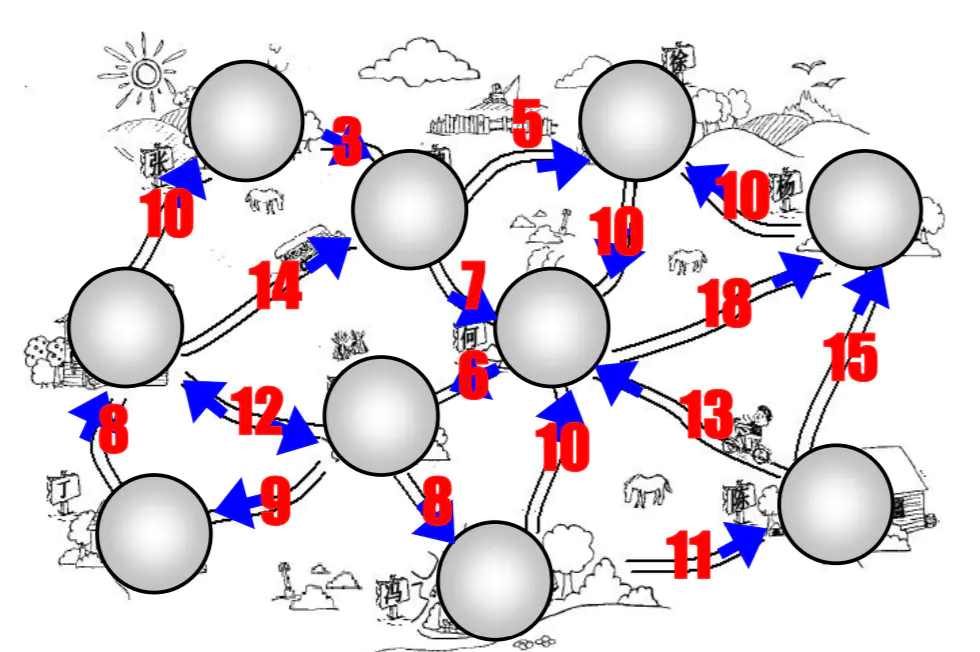
    • 这里的权重可以是任意你希望表示的数据：比如距离或者花费的时间或者票价。
    • 我们来看一张有向和带权的图
      image

现实建模

  • 对交通流量建模

    • 顶点可以表示街道的十字路口，边可以表示街道.。
    • 加权的边可以表示限速或者车道的数量或者街道的距离。
    • 建模人员可以用这个系统来判定最佳路线以及最可能堵车的街道。

  • 对飞机航线建模

    • 航空公司可以用图来为其飞行系统建模。
    • 将每个机场看成顶点，将经过两个顶点的每条航线看作一条边。
    • 加权的边可以表示从一个机场到另一个机场的航班成本，或两个机场间的距离。
    • 建模人员可以利用这个系统有效的判断从一个城市到另一个城市的最小航行成本。
      ​

二、图的表示

我们知道一个图包含很多顶点，另外包含顶点和顶点之间的连线（边），这两个都是非常重要的图信息，因此都需要在程序中体现出来。

顶点表示

  • 顶点的表示相对简单

    • 上面的顶点，我们抽象成了 1 2 3 4，也可以抽象成 A B C D。在后面的案例中，我们使用 A B C D。
    • 那么这些 A B C D 我们可以使用一个数组来存储起来(存储所有的顶点)。
    • 当然，A B C D 有可能还表示其他含义的数据(比如村庄的名字)，这个时候，可以另外创建一个数组，用于存储对应的其他数据。

  • 边的表示略微复杂

    • 因为边是两个顶点之间的关系，所以表示起来会稍微麻烦一些。
    • 下面是变常见的表示方式。

邻接矩阵

  • 概述

    • 邻接矩阵让每个节点和一个整数向关联, 该整数作为数组的下标值.
    • 我们用一个二维数组来表示顶点之间的连接.
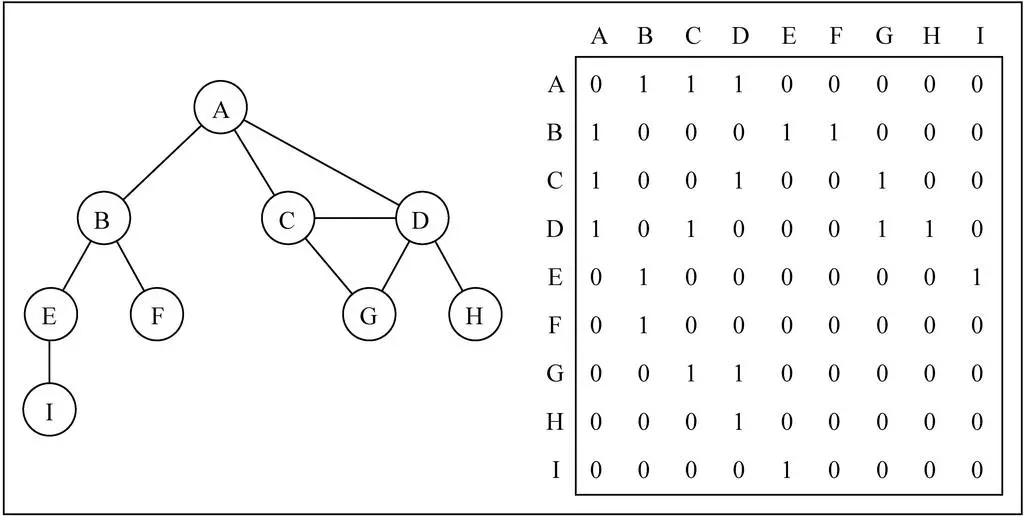
    • 演示
      image

  • 图片解析

    • 在二维数组中，0 表示没有连线，1 表示有连线。
    • 通过二维数组，我们可以很快的找到一个顶点和哪些顶点有连线。（比如 A 顶点, 只需要 遍历第一行即可）
    • 另外，A - A，B - B（也就是顶点到自己的连线），通常使用 0 表示。

  • 邻接矩阵的问题

    • 如果是一个无向图，邻接矩阵展示出来的二维数组，其实是一个对称图。

      • 也就是 A -> D 是 1 的时候，对称的位置 D -> 1 一定也是 1。
      • 那么这种情况下会造成空间的浪费，解决办法需自己去研究下。

    • 邻接矩阵还有一个比较严重的问题就是如果图是一个稀疏图

      • 那么矩阵中将存在大量的 0，这意味着我们浪费了计算机存储空间来表示根本不存在的边。
      • 而且即使只有一个边，我们也必须遍历一行来找出这个边，也浪费很多时间。

邻接表

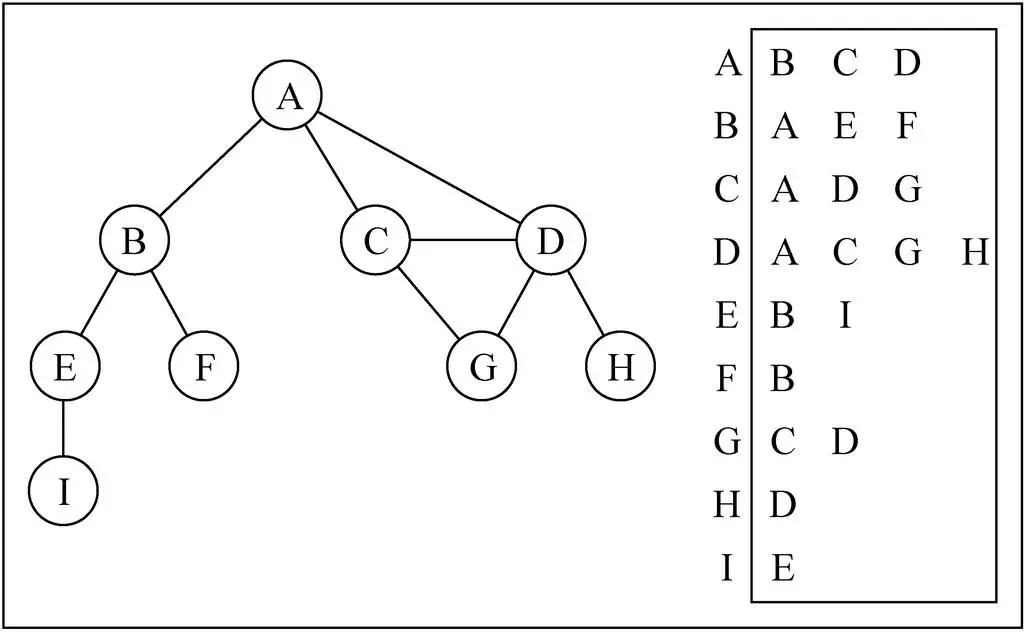
  • 概述

    • 邻接表由图中每个顶点以及和顶点相邻的顶点列表组成。
    • 这个列表有很多中方式来存储：数组/链表/字典(哈希表)都可以。
    • 演示
      image

  • 图片解析

    • 其实图片比较容易理解
    • 比如我们要表示和 A 顶点有关联的顶点（边），A 和 B/C/D 有边，那么我们可以通过 A 找到 对应的数组/链表/字典，再取出其中的内容就可以啦。

  • 邻接表的问题

    • 邻接表计算“出度”是比较简单的（出度：指向别人的数量, 入度: 指向自己的数量）
    • 邻接表如果需要计算有向图的“入度”，那么是一件非常麻烦的事情。
    • 它必须构造一个“逆邻接表”，才能有效的计算“入度”。而临街矩阵会非常简单。

三、图的封装

创建图类

  • 先来创建 Graph 类，定义了两个属性：
    • vertexes 用于存储所有的顶点，使用一个数组来保存。
    • adjList adj 是 adjoin 的缩写，邻接的意思。adjList 用于存储所有的边，这里采用邻接表的形式。
1
2
3
4
5
6
class Graph {
  constructor() {
    this.vertexes = []; // 存储顶点
    this.adjList = new Dictionay(); //存储边信息
  }
}

添加方法

  • 添加顶点：可以向图中添加一些顶点。
    • 将添加的顶点放入到数组中。
    • 另外，给该顶点创建一个数组[]，该数组用于存储顶点连接的所有的边.（回顾邻接表的实现方式）
1
2
3
4
5
6
7
// 添加顶点
addVertex(val) {
    // 添加点
    this.vertexes.push(val)
    // 添加点的关系  采用邻接矩阵法 结构用Map
    this.adjList.set(val, [])
}
  • 添加边：可以指定顶点和顶点之间的边。
    • 添加边需要传入两个顶点，因为边是两个顶点之间的边，边不可能单独存在。
    • 根据顶点 v 取出对应的数组，将 w 加入到它的数组中。
    • 根据顶点 w 取出对应的数组，将 v 加入到它的数组中。
    • 因为这里实现的是无向图，所以边是可以双向的。
1
2
3
4
5
6
7
// 添加边
addEdge(val1, val2) {
    // 添加边需要传入两个顶点, 因为边是两个顶点之间的边, 边不可能单独存在.
    // 这里实现的是无向图, 所以这里不考虑方向问题
    this.adjList.get(val1).push(val2)
    this.adjList.get(val2).push(val1)
}

toString 方法：为了能够正确的显示图的结果，就是拿出二维数组的每一项。

1
2
3
4
5
6
7
8
9
10
11
12
13
// 输出图结构
toString() {
    let res = ''
    for (let i = 0; i < this.vertexes.length; i++) {
        res += this.vertexes[i] + "->"
        let adj = this.adjList.get(this.vertexes[i])
        for (let j = 0; j < adj.length; j++) {
            res += adj[j] + ""
        }
        res += "\n"
    }
    return res
}

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 测试代码
let graph = new Graph();

// 添加顶点
let myVertexes = ["A", "B", "C", "D", "E", "F", "G", "H", "I"];
for (let i = 0; i < myVertexes.length; i++) {
  graph.addVertex(myVertexes[i]);
}

// 添加边
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("A", "D");
graph.addEdge("C", "D");
graph.addEdge("C", "G");
graph.addEdge("D", "G");
graph.addEdge("D", "H");
graph.addEdge("B", "E");
graph.addEdge("B", "F");
graph.addEdge("E", "I");

四、图的遍历

和其他数据结构一样，需要通过某种算法来遍历图结构中每一个数据。这样可以保证，在我们需要时，通过这种算法来访问某个顶点的数据以及它对应的边。

遍历的方式

  • 图的遍历思想
    图的遍历算法的思想在于必须访问每个第一次访问的节点，并且追踪有哪些顶点还没有被访问到。

  • 有两种算法可以对图进行遍历

    • 广度优先搜索(Breadth-First Search, 简称 BFS)
    • 深度优先搜索(Depth-First Search, 简称 DFS)
    • 两种遍历算法，都需要明确指定第一个被访问的顶点。

  • 遍历的注意点

    • 完全探索一个顶点要求我们便查看该顶点的每一条边。
    • 对于每一条所连接的没有被访问过的顶点，将其标注为被发现的，并将其加进待访问顶点列表中。
    • 为了保证算法的效率：每个顶点至多访问两次。

  • 两种算法的思想

    • BFS 基于队列，入队列的顶点先被探索。
    • DFS 基于栈，通过将顶点存入栈中，顶点是沿着路径被探索的，存在新的相邻顶点就去访问。

  • 为了记录顶点是否被访问过，我们使用三种颜色来反应它们的状态。(或者两种颜色也可以)

    • 白色表示该顶点还没有被访问.
    • 灰色表示该顶点被访问过, 但并未被探索过.
    • 黑色表示该顶点被访问过且被完全探索过.
    • 初始化颜色代码
1
2
3
4
5
6
7
8
9
10
11
// 初始化顶点的颜色
_initializeColor() {
    // 白色: 表示该顶点还没有被访问.
    // 灰色: 表示该顶点被访问过, 但并未被探索过.
    // 黑色: 表示该顶点被访问过且被完全探索过.
    let colors = []
    for (let i = 0; i < this.vertexes.length; i++) {
        colors[this.vertexes[i]] = "white"
    }
    return colors
}

广度优先搜索(BFS)

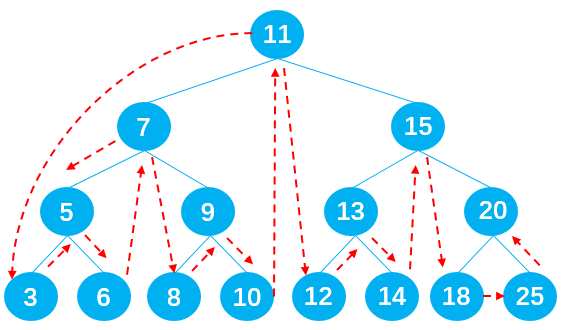
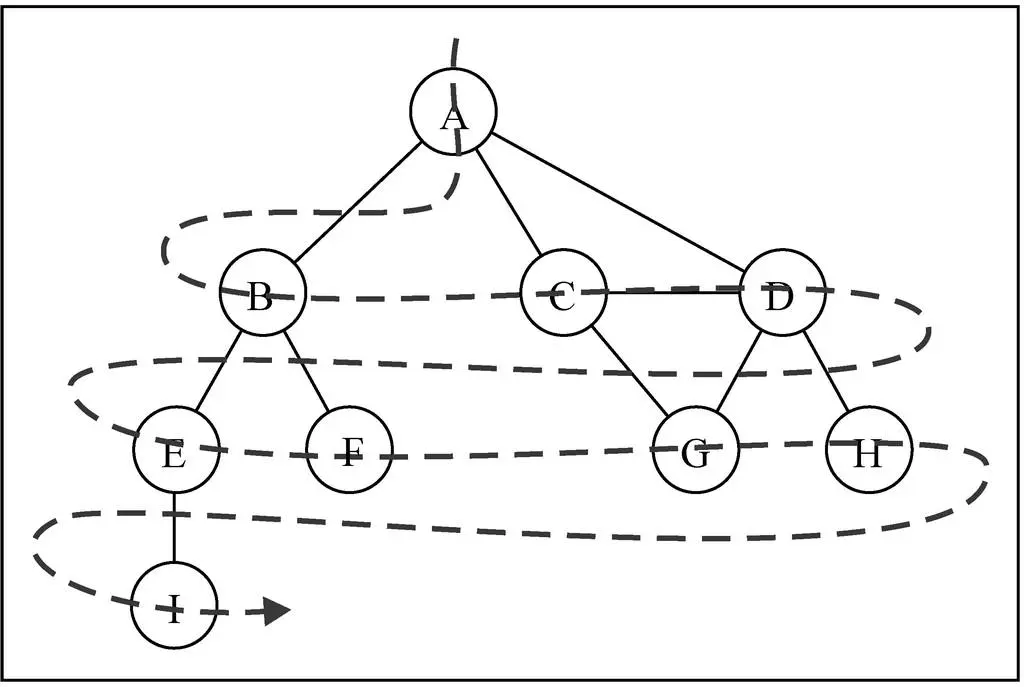
  • 广度优先搜索算法的思路
    广度优先算法会从指定的第一个顶点开始遍历图，先访问其所有的相邻点，就像一次访问图的一层。换句话说，就是先宽后深的访问顶点。

  • 图解 BFS
    image

  • 广度优先搜索的实现

    1. 创建一个队列 Q
    2. 将 v 标注为被发现的(灰色), 并将 v 将入队列 Q
    3. 如果 Q 非空, 执行下面的步骤：
      • 将 v 从 Q 中取出队列
      • 将 v 标注为被发现的灰色
      • 将 v 所有的未被访问过的邻接点（白色），加入到队列中
      • 将 v 标志为黑色

  • 广度优先搜索的代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    // 广度优先搜索
    bfs(handle) {
        // 1.初始化颜色
        let color = this._initializeColor()
        // 2. 创建队列
        let queue = new Queue
        // 3. 将传入的顶点放入队列
        queue.enqueue(this.vertexes[0])
        // 4.依赖队列操作数据   队列不为空时一直持续
        while (!queue.isEmpty()) {
            // 4.1 拿到队头
            let qVal = queue.dequeue()
            //  4.2 拿到队头所关联（相连）的点并设置为访问中状态（灰色）
            let qAdj = this.adjList.get(qVal)
            color[qVal] = "gray"
            // 4.3 将队头关联的点添加到队尾
            // 这一步是完成bfs的关键，依赖队列的先进先出的特点。
            for (let i = 0; i < qAdj.length; i++) {
                let a = qAdj[i]
                if (color[a] === "white") {
                    color[a] = "gray"
                    queue.enqueue(a)
                }
            }
            // 4.5设置访问完的点为黑色。
            color[qVal] = "black"
            if (handle) [
                handle(qVal)
            ]
        }
    }

  • 测试代码

    1
    2
    3
    4
    5
    6
    // 调用广度优先算法
    let result = "";
    graph.bfs(graph.vertexes[0], function (v) {
      result += v + " ";
    });
    console.log(result); // A B C D E F G H I

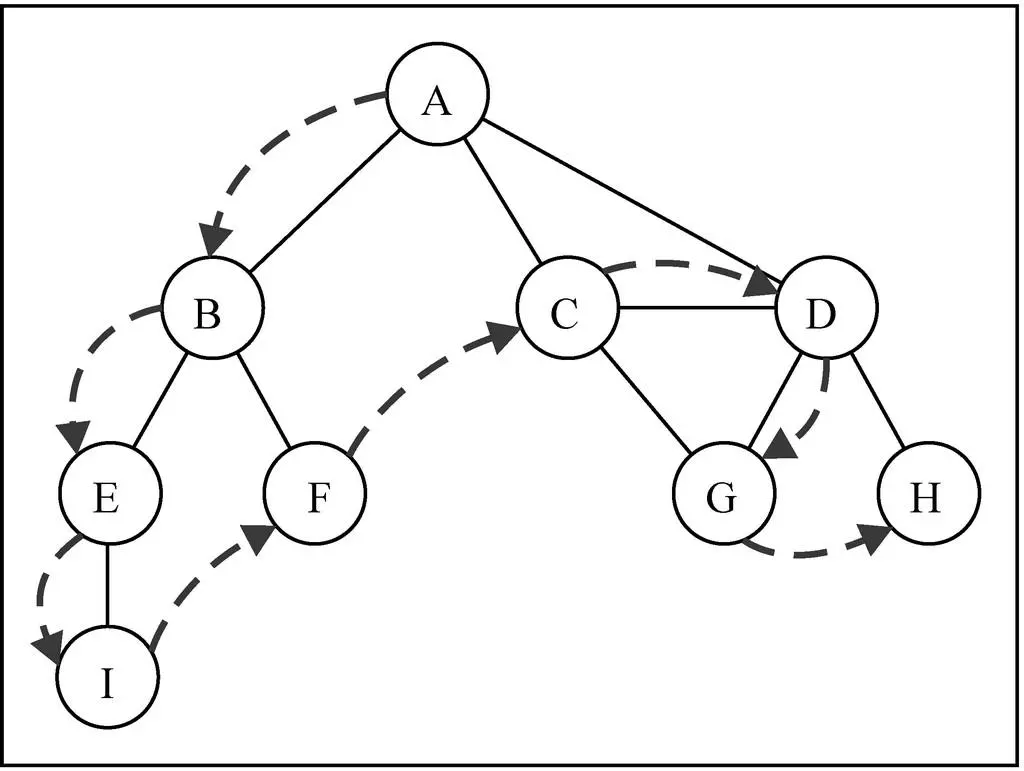
深度优先搜索(DFS)

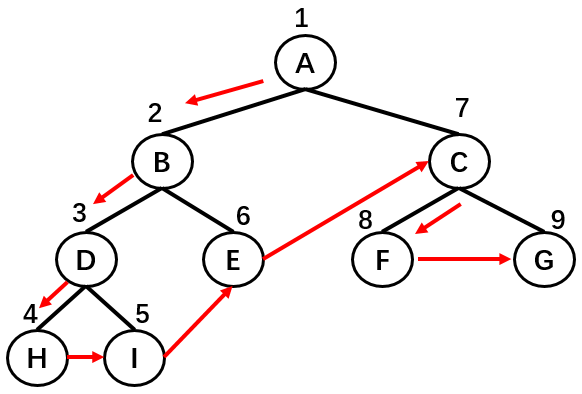
深度优先搜索的思路：

  • 深度优先搜索算法将会从第一个指定的顶点开始遍历图，沿着路径知道这条路径最后被访问了。
  • 接着原路回退并探索吓一条路径。
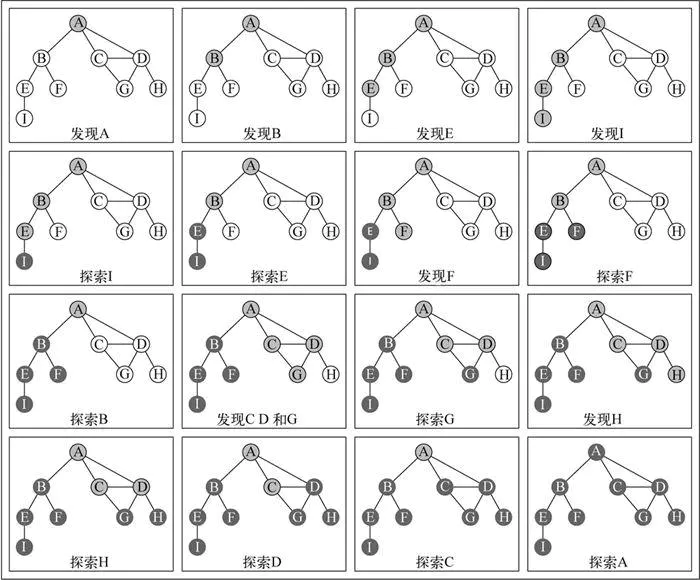
  • 图解 DFS
    image

深度优先搜索算法的实现：

  • 广度优先搜索算法我们使用的是队列，这里可以使用栈完成，也可以使用递归。

  • 方便代码书写，我们还是使用递归(递归本质上就是函数栈的调用)

  • 深度优先搜索算法的代码：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    // 深度优先搜索
    dfs(handle) {
        // 1.初始化颜色
        let color = this._initializeColor()
        // 2. 遍历所有顶点，开始访问
        for (let i = 0; i < this.vertexes.length; i++) {
            if (color[this.vertexes[i]] === "white") {
                this._dfsVisit(this.vertexes[i], color, handle)
            }
        }
    }
    // dfs的递归方法  这里直接使用函数的调用栈
    _dfsVisit(val, color, handle) {
        // 1. 将颜色设置为访问中
        color[val] = "gray"
        // 2. 执行相应的回调
        if (handle) {
            handle(val)
        }
        // 3. 拿与该点相邻的点，对每个点操作
        let adj = this.adjList.get(val)
        for (let i = 0; i < adj.length; i++) {
            let w = adj[i]
            // 如果相邻点未未访问状态，开始访问。
            if (color[w] === "white") {
                this._dfsVisit(w, color, handle)
            }
        }
        // 4. 处理完后设置为访问过点。
        color[val] = "black"
    }

  • 测试代码

    1
    2
    3
    4
    5
    6
    7
    // 调用深度优先算法
    result = "";
    graph.dfs(function (v) {
      result += v + " ";
    });
    // 输出深度优先
    console.log(result); //A B E I F C D G H

  • 递归的代码较难理解一些，这副图来帮助理解过程：
    image